Mocninové funkcie

Mocninové funkcie sú celá skupina funkcií, ktoré majú spoločný zápis. $$y = ax^n$$ Líšia sa v exponente. Čo iné číslo v exponente, to iná funkcia. V tomto článku sa pozrieme na to, ako jednotlivé čísla, či skôr skupiny čísiel ovplyvňujú chovanie funkcie. No ešte skôr si povieme niečo o histórii a využití mocninových funkcii, aby sa lepšie dalo pochopiť, že odkiaľ prišli a na čo sú.

História mocninových funkcií

Mocninové problémy ľudia poznali už na úsvite civilizácie. Napríklad toto je staroegyptská úloha nájdená na Rhindskom papyruse:



Problémy, kde sa vyskytovali mocniny vyššieho rádu boli však zriedkavé. Ľudia sa väčšinou stretávali s mocninami $x^1, x^2, x^3$. V bežnom živote riešili iba meranie dĺžok, obsahov a objemov, a tak im toto stačilo. Síce ešte kde tu nájdeme zmienku aj o problémoch s mocninami vyššieho rádu, ale sú skôr na zábavu ako na úžitok. Na riešenie problémov používali iba nejaké slovné postupy, nemali zavedený žiaden formálny zápis matematiky.

Egypťania a Babylončania využívali mocninové problémy iba z čisto praktického hľadiska. Trochu teórie pridali k mocninám Gréci, keď spravili geometrické vysvetlenie druhej a tretej mocniny. V 9. storočí pridali svoju trošku aj Araby, keď urobili algebraické riešenie kvadratickej a kubickej rovnice. Riešenie kvartickej rovnice priniesla až renesancia.[2][3]

Doteraz sme sa bavili iba o rovniciach nižšieho rádu, ktoré boli riešené nejakou algebraickou metódou. Avšak až teraz sa mocninové funkcie začínajú podobať tomu, čo poznáme dnes. Ich praktické použitie bude pravdepodobne stále minimálne. Mocniny sa budú rozvíjať hlavne vďaka rozvoju matematickej teórie. Možno sa sem tam objavia pri práci s veľkými číslami, ale prácu nasledovných ľudí skutočne ocení až rozmach fyziky, kedy sa veľké exponenty objavia pri opise rozličných fyzikálnych zákonov. O tom si povieme však neskôr. Teraz sa pozrieme na ľudí, vďaka ktorým dnes tieto zákony vieme opísať.

💰 1445 - 1500 Nicolas Chuquet: bol francúzsky matematik, ktorý sa zaoberal veľkými číslami (lebo asi obchodovanie). Vďaka tomu sa musel venovať aj mocninám, pretože sa mu nechcelo stále písať dlhé čísla. Vymyslel si svoju notáciu (zápis) mocnín. Pri práci s nimi si všimol isté súvislosti a spravil prvú verziu jedného z pravidiel exponentov: $x^m \cdot x^n = x^{m+n}$. Tiež si všimol, že exponent by mohol byť aj záporné alebo racionálne číslo.[4]

🎓 1487 - 1567 Michael Stifel: bol to pre zmenu nemecký matematik a tiež sa zaoberal mocninami. Ako prvý použil slovo "exponent". Rozšíril pravidlá pre exponenty, ktoré začal Chuquet. Vylepšil pravidlo $x^m \cdot x^n = x^{m+n}$ tak, že sa už hodilo aj na záporné čísla. Spravil pravidlo $x^m / x^n = x^{m-n}$. Tiež urobil pravidlo, že $x^0 = 1$.[5]

√ 1499 - 1545 Christoph Rudolff: bol nemecký matematik a zaviedol symbol pre odmocninu $\sqrt{}$. Traduje sa, že tento symbol má pôvod v písmene "r", čo je začiatočné písmeno latinského slova "radix" - koreň. Neskôr, bola k písmenu pridaná tá dlhá horizontálna čiara, aby bolo jasné, čo všetko je pod odmocninou.[6]

🔠 1540 - 1603 Francois Viéte: ďalší francúzsky matematik. Pridal do matematiky písmenká a nejaké iné divné značky. Krajšie povedané, zaviedol symbolizmus.[7]

📐1596 - 1650 René Descartes: zase ďalší francúzsky matematik, ktorý sa zaoberal tým, že sa snažil previesť geometrické úlohy na algebraické (akože napríklad Pytagorovu vetu nenarysuješ, ale vyrátaš vzorcom). Keďže už bol vďaka Viétemu v matematike zavedené formálny zápis, tak Descartes mohol na ňom stavať. Jednou z vecí, ktoré spravil bolo, že celkom dobre zjednotil zápis pre mocniny. Čo sa týka exponentov, tak dôveroval iba prirodzeným číslam.[8]

🔑 1616 - 1703 John Wallis: toto bol anglický matematik. Bol jeden z tých, ktorý robili na kalkuluse, ale nehovorí sa o nich tak ako Newtonovi s Leibnizom. Pri svojej práci potreboval exponenty a tak vylepšil trochu aj tie. Pravidlá pre exponenty rozšíril o záporné a racionálne exponenty, a sformalizoval použitie exponentov pre rôzne typy čísiel.[9]

🍎 1643 - 1727 Isaac Newton: tiež anglický matematik, tiež robil na kalkuluse a tiež zjavne potreboval exponenty. Pozberal prácu predošlých matematikov, niečo pridal svoje a bol jeden z prvých, ktorý začali používať exponenty v reálnej práci, vrátane záporných a racionálnych exponentov.[10]

Ďalší osud mocninových funkcií je podobný osudu ostatných funkcií. Vietého písmenká, Descartova analytická geometria, Newtonov infintenzimálny počet, Eulerova kniha Introductio in analysin infinitorum a ďalší, čoraz podrobnejší výskum funkcií ako funkcií. Celú históriu funkcií nájdeš podrobnejšie opísanú tu.

Použitie mocninových funkcií

S mocninovými funkciami nižšieho rádu sa dá stretnúť ľahšie. Staroveké národy sa stretali s dĺžkami, obsahmi a objemami. Preto sa dlhé tisícročia riešili iba problémy, ktoré dnes voláme lineárne ($x^1$), kvadratické ($x^2$) a kubické ($x^3$). Vyššie mocniny prišli do hry až v 15. storočí s rozvojom matematickej teórie. Až neskôr, keď sa vyvinula vyššia fyzika, aj mocniny s veľkými exponentmi našli svoje uplatnenie v reálnom živote.

Úplne bezprostredne sa s mocninovými funkciami dá stretnúť v bežnom živote ťažko. Opisujú správanie, ktoré sa zvyčajne nevyskytuje. Stretneš sa s ním, až keď pôjdeš študovať za inžiniera, prírodovedca alebo niečo podobné. Preto tu vymenujeme len zopár príkladov použitia, ale nebudeme sa púšťať do ich bližšieho vysvetľovania.

🌉 Priehyb nosníka: v stavebníctve sa používajú na vypočítanie toho, ako sa môže nosník ohnúť pod záťažou.[11]

⚛ Van der Waalsove sily: sú to sily, ktoré sú v interakciách medzi molekulami alebo atómami. Na časť výpočtov sa tam používa Lennard-Jonesov potenciál, a práve tu sa používajú mocninové funkcie vyššieho rádu.[12]

🌍 Životné prostredie: v oblasti veľkých miest býva dosť znečistený vzduch. Veľkým zdrojom znečistenia sú diaľnice. Vedci sa pozreli na jednu z diaľnic v okolí Šanghaja a skúmali, ako sa škodliviny šíria ovzduším. Zistili, že sa to dá modelovať mierne upraveným mocninovým zákonom.[13]

🤖 Robotika: ďalšie uplatnenie našiel mocninový zákon v robotike. Presnejšie pri robotoch, ktorý vykonávajú chirurgické operácie. Vedci sa snažili prísť na to, ako by sa mohli operujúci roboti hýbať čo najlepšie a najjemnejšie. Skúmali pohyby ľudskej ruky a uvedomili si, že tie pohyby sa dajú opísať mocninovým zákonom.[14]

🍅 Ne-Newtonovské kvapaliny: sú to kvapaliny, ktoré sa nesprávajú podľa Newtonovských zákonov viskozity. To znamená, že ich viskozita (snaha tiecť) sa mení podľa toho, ako na ne pôsobí sila. Príkladom je kečup. Keď sa iba tak jemne tlačí z fľašky, tak je hustý. Ale keď sa fľaška poriadne zatrasie, tak je redší. Toto bolo o ne-Newtonovských kvapalinách vážne. A teraz buďme trochu deti. Keď sa v správnom pomere zarobí voda a nejaký škrob, tak dostaneme takú tekutinu, že keď do nej iba pomaličky vložíme ruku, tak sa rozleje ako voda. Ale keď sa do toho silno buchne, tak sa to správa, ako keby človek búchal do steny.

Mocninové funkcie

Ako vidieť, s mocninovými funkciami prídeme v bežnom živote do styku ťažko. Preto si ich tento raz ani nebudeme vysvetľovať na príkladoch, ale pozrieme sa na ne čisto z matematického hľadiska. Postupným vývojom mocninové funkcie dostali zápis, aký poznáme dnes: $$y = ax^n$$ Písmeno y je výsledok funkcie, x sú čísla, ktoré do nej dávam (je to premenná), a je nejaká konštanta a n je exponent. Teraz sa chvíľu povenujeme tomu exponentu, pretože je to taká hlavná charakteristika mocninovej funkcie.

Exponent môže byť hocijaké číslo. Môže byť kladný, záporný, môže to byť nula alebo zlomok. Dokonca to môže byť aj iracionálne alebo komplexné číslo. Teraz sa však takýmto obludnostiam nebudeme venovať a pozrieme sa iba na prípady, kedy je exponent buď kladné celé číslo, záporné celé číslo, racionálne číslo alebo nula. Každý z týchto prípadov je trochu iný.

Mocninové funkcie s prirodzeným exponentom

Tieto funkcie majú v exponente prirodzené číslo. Ak by náhodou, tak prirodzené čísla sú, že 1,2,3,4 a takto ďalej až po nekonečno. Prirodzený exponent ľudia objavili ako prvý, pretože si ním iba skrátili zápis násobenia. Keď mali napríklad číslo 5 vynásobiť osemkrát, tak namiesto 5*5*5*5*5*5*5*5, napísali $5^8$.

Tu sa exponenty delia ešte na párne a nepárne, pretože každý prináša iné správanie funkcie. Je to kvôli násobeniu, pretože keď sa záporné číslo násobí párny počet krát, tak bude z toho kladné číslo a keď sa násobí nepárny počet krát, tak je z toho záporné číslo. Napríklad $(-3)\cdot(-3)=9$ a $(-3)\cdot(-3)\cdot(-3)=-27$ (lebo mínus krát mínus je plus...).

Pozrieme sa na pár funkcí v tabuľke:

V grafe si môžeš vyskúšať zmeniť exponenty a porovnať medzi sebou funkciu s párnym a nepárnym exponentom. Máme tu aj pár otázok, ktoré si môžeš pre svoj dobrý pocit zodpovedať. Doporučujeme si veci vypočítať pre pár konkrétnych hodnôt a aj si nakresliť nejaký ten graf.





Mocninové funkcie s prirodzeným exponentom sa dajú podľa svojho správania rozdeliť na dva druhy. Na tie, ktoré majú exponent párny a na tie, ktoré ho majú nepárny. Je to spôsobené tým, že keď sa nejaké číslo násobí samým sebou párny počet krát, tak výsledok bude vždy párny. Aj keď to číslo bude záporné, pretože mínus krát mínus je plus. Takáto funkcia bude vracať pre záporné aj kladné čísla vždy kladné číslo. Jej graf bude teda pripomínať písmenko U.

Keď je exponent nepárny, tak pre záporné čísla bude funkcia vracať záporné hodnoty a pre kladné bude vracať kladné hodnoty. Je to preto, lebo keď sa záporné číslo bude nepárny počet razy násobiť samým sebou, tak výsledok je záporný. Skús si len tak pre seba vyrátať (-4)⁵ a (-4)⁶.

Pre párny aj nepárny exponent platí, že čím bude väčší, tým bude graf strmší. Je to preto, lebo čím sú čísla ďalej od nuly, tým majú rovnako vzdialený susedia väčšie rozdiely medzi hodnotami. Vyrátaj si prosím hodnoty pre tieto čísla a porovnaj rozdiely medzi nimi: 2², 3², 51², 52² a 2⁵, 3⁵, 51⁵, 52⁵.

Určite si si všimol, že medzi mocninové funkcie s prirodzeným exponentom patria funkcie s exponentom 1, 2 a 3. Teda $x^1, x^2, x^3$. Iste ti pripomínajú lineárnu, kvadratickú a kubickú funkciu. Pripomínajú ti to správne. Tieto tri druhy mocninových funkcií majú svoje pomenovania preto, lebo ľudia sa nimi zaoberali dávno predtým, než sa prišlo na nejaké mocniny a exponenty. Niečo, čo sa vyvinulo do lineárnej funkcie ľudia používali na rátanie s dĺžkami. Predchodcovia kvadratickej funkcie opisovali problémy s počítaním plôch. Na rátanie objemov zas používali postupy, ktoré časom vyústili do kubickej funkcie.

Mocninová funkcie s nulou v exponente

Ak máme funkciu $y = x^0$, tak čokoľvek sa dosadí za x, bude 1. Vyplýva to z jedného z exponenciálnych pravidiel, na ktoré prišli týpci okolo 17. storočia.

Tu sa môžeš zamyslieť nad úlohou a pohrať sa s grafom, ale na tejto funkcii asi ani nie je veľmi ako.

Mocninové funkcie so záporným exponentom

Tieto funkcie majú v exponente záporné číslo. Podobne, ako predchádzajúca funkcia, aj tieto vznikli vďaka exponenciálnym pravidlám.

Tu je tabuľka, kde si môžeš vyrátať zopár výsledkov pre dve mocninové funkcie so záporným exponentom, aby si vedel, ako to funguje. Keď klikneš, budú tam výsledky, ale prosím neklikaj skôr, ako to aspoň skúsiš vyrátať.

Tu sa môžeš vyblázniť na grafe a zodpovedať nasledovné otázky.





Mocninové funkcie so záporným exponentom ($\frac{1}{x^n}$) nie sú definované na celom obore reálnych čísiel. To znamená, že za x môžeš dosadiť skoro všetko, okrem nuly. Tá sa tam nedá dosadiť kvôli tomu, že by v menovateli vyšla nula a z materskej školy vieme, že nulou sa deliť nedá. Čím sa dosadí číslo bližšie k nule, tým zlomok vyjde väčší a teda aj hodnota funkcie je väčšia. Čím viac budeme ďalej od nuly, tým sa bude deliť väčším číslom a teda aj zlomok vyjde menší. Grafy majú taký hokejkový tvar, pretože od nuly po jedna rastú rýchlo a od jednotky už pomalšie. To, či bude funkcia vracať kladné aj záporné hodnoty alebo iba kladné, záleží na tom, či je exponent párny alebo nepárny. Pri nepárnom exponente môže vrátiť kladné aj záporné čísla a pri párnom iba kladné. Že prečo? Máme to napísané pri mocninových funkcia s prirodzeným exponentom, tak sa pozri tam.

Mocninové funkcie s racionálnym exponentom - odmocniny

Táto kapitola bude trochu dlhšia, pretože tu sa budeme baviť aj o odmocninách. O odmocninách preto, lebo odmocniny sú mocninové funkcie s racionálnym exponentom.

N-tá odmocnina je vlastne číslo, ktoré keď sa n-krát vynásobí medzi sebou, tak dostaneme to číslo, z ktorého sa robí tá odmocnina. Napríklad druhá odmocnina zo 100 je 10, pretože 10*10=100 alebo piata odmocnina zo 16 807 je 7, pretože 7*7*7*7*7 je 16 807, alebo tretia odmocnina z 27 je 3, pretože 3*3*3 je 27. Úlohou n-tej odmocniny je zobrať nejaké číslo (napr. 100, 16 807, 27) a nájsť také číslo, že keď to sa n-krát vynásobí samým sebou, tak dostanem to pôvodné číslo.

Ako skoro vždy, všetko sa to začalo už v starovekom Egypte. Už sme sa bavili o tom, že Egypťania riešili mocninové problémy. Napríklad, že keď mám roľu veľkú 10*10 metrov, aký je jej obsah? Ale riešili aj opačné problémy a tie nás budú zaujímať. Keď vedeli, že majú štvorcovú roľu veľkú 100m², chceli zistiť, aké veľké sú jej strany. Tu niekde začínajú problémy s odmocninou. Egyptské znalosti rozšírili Gréci s geometriou a neskôr Araby s algebrou.

Nie všetky čísla majú odmocninu peknú, že je to nejaké celé číslo. Napríklad odmocnina z dvojky je iracionálna a to sa nikomu zapisovať nechce. A takých škaredých odmocnín je veľmi veľa. Počas renesancie sa rátanie odmocnín stalo asi dosť časté a tak si ľudia zjednodušili zápis. Namiesto rátania odmocniny si iba poznačili, že tu má byť odmocnina z nejakého čísla.

Tento krajší zápis je zo 16-teho storočia. Nemecký matematik Christoph Rudolf začal označovať korene kvadratickej rovnice (druhú odmocninu) malým písmenkom r, čo je začiatočné písmeno latinského slova radix - koreň. Neskôr sa tá horná čiara v r-ku predĺžila, aby bolo jasne vidno čo je pod odmocninou a postupne vznikol z toho dnešný symbol $\sqrt[n]{ }$.

Keď sa neskôr ľudia bavili s pravidlami pre exponenty, tak prišli na to, že problém odmocniny sa dá zapísať aj pomocou týchto pravidiel, a že teda odmocnina je vlastne druh exponentu.

Keď už vieš, čo je odmocnina, môžeš si ich zopár vyrátať do tabuľky, ...

...vyriešiť nasledujúce úlohy...

...a vyskúšať si ich na grafe...

Prv než pôjdeme rozoberať nejaké vlastnosti funkcií, treba sa dohodnúť na jednej veci. Odmocniny môžu mať viacero možných riešení, a teda nemôžu byť funkcie. Pretože ak chceme niečo nazývať funkciou treba, aby to dávalo pre jeden vstup práve jeden výstup. A odmocniny ich dajú viac (napr.: $\sqrt{4} = \pm 2$). Preto sa budeme opierať o všeobecnú dohodu, že ak chceme s odmocninou pracovať ako s funkciou, budeme brať iba ten výsledok, ktorý patrí do kladných reálnych čísiel.

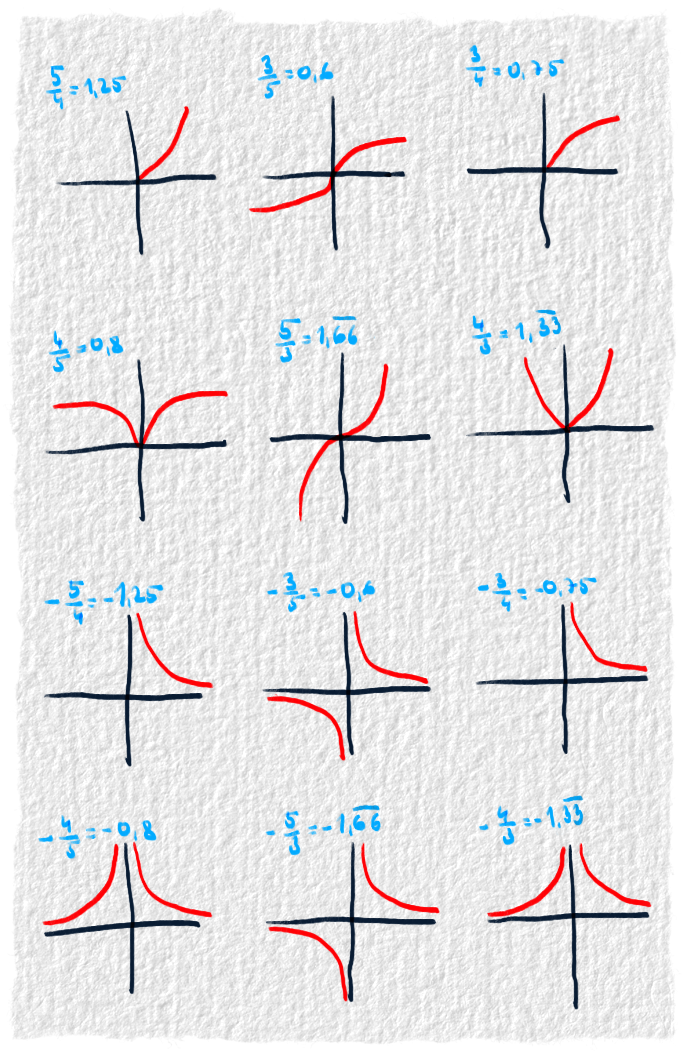
Správanie mocninových funkcií s racionálnym exponentom sa dá rozdeliť do dvanástich kategórii. Všetko záleží na exponente. Na tom, či je kladný alebo záporný. Či je väčší ako 1, menší ako -1 alebo sa nachádza niekde medzi -1 a 0 či medzi 0 a 1. Aj na tom, či sú v zlomku čísla párne alebo nepárne.

Keďže správanie funkcie závisí na tom, či je exponent párny alebo nepárny, treba dávať pozor, aby bol zlomok v základnom tvare. Lebo keď je niečím vynásobený, tak sa tam čachruje s párnosťou a nepárnosťou a to nerobí dobrotu. Nepýtaj sa prečo, je to príliš komplikované. Ber to ako fakt, proste keď nie je zlomok v základnom tvare, vznikajú tam blbosti. Možno sa to niekedy pozrieme, ale zatiaľ to necháme na pokoji.

Ako sa ráta odmocnina

Vyrátať napríklad $5^2$ je ľahké, pretože sa iba 2-krát vynásobí päťka sama so sebou. Dokonca aj $5^{-2}$ je ľahké, lebo to sa dá iba $\frac{1}{5^2}$. Horšie je už spraviť $5^{\frac{1}{2}}$. Vynásobiť päťku pol-krát sebou samou, to sa ťažko predstavuje.

👏 2000 BC - Starovekým národom sa tiež z toho zamotala hlava, ale nakoniec si dali rady celkom dobre. Postup, ktorý vymysleli, používajú na výpočet odmocniny aj dnešné počítače. Už je samozrejme vylepšený storočiami, ktoré prešli od Babylončanov až po nás, ale princíp zostáva.[15]

🏺 1650 BC - Egypťania rátaniu odmocnín moc nedali a ich postupy boli na rozdiel od kolegov z Babylonskej ríše viac chaotické. Odmocniny viac-menej iba odhadovali.[16]

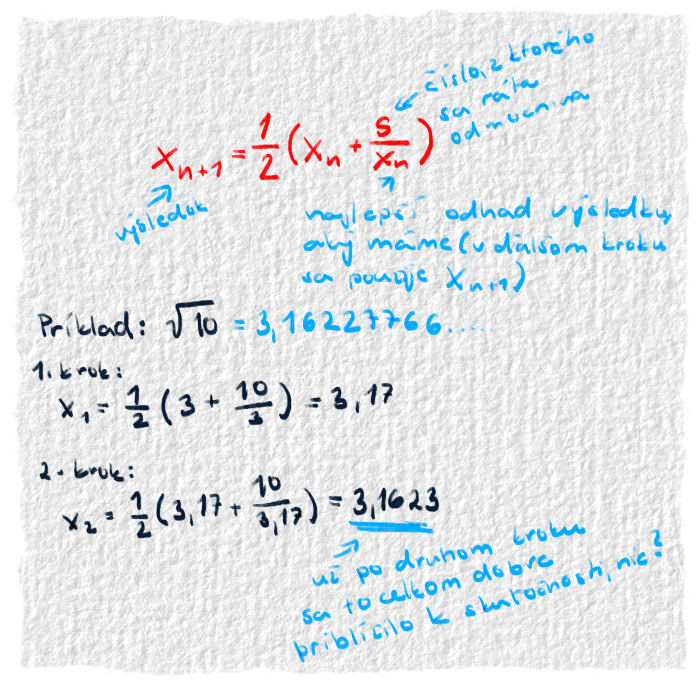
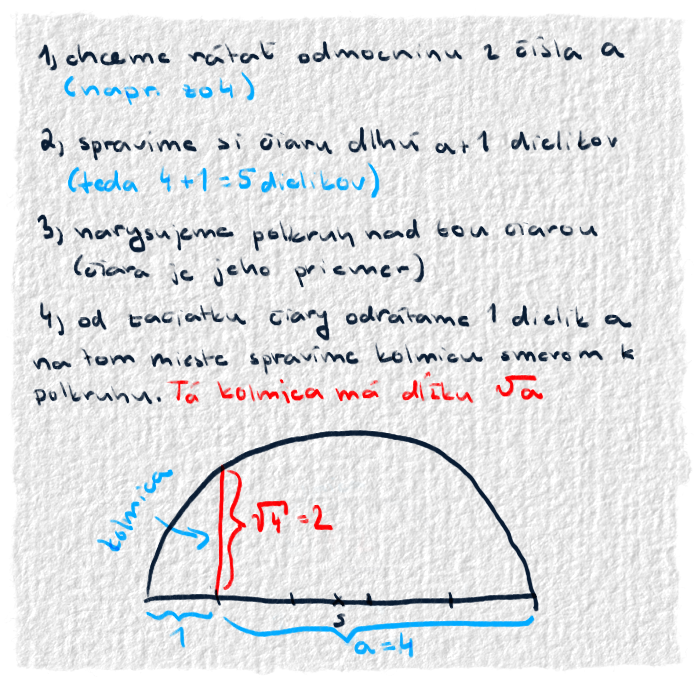
🏛️ 600 BC - 300 AD - V tomto období prispeli k odmocninám aj Gréci. Po zrážke s iracionálnymi číslami Gréci zanevreli na algebru a všetko riešili geometricky. A teda aj nájdenie odmocniny bude geometrické. Ich postup je opísaný na obrázku.[17]

⚔ Rimania nespravili na matematike dokopy nič. Skoro všetko poznanie udržiavajú Gréci, ale ani tí nič moc aktívne nevyvíjajú. Po rozpade Rímskej ríše sa ich vedomosti presúvajú na východ.

🐘 500 AD - Indický matematik Brahmagupta vyvinul algoritmy pre rátanie druhej a tretej odmocniny. Už to nebola geometria, ale bola to taká algebra v plienkach. Jeho postupy boli opísané slovne.[18]

🐫 820 AD - Z Indie sa presúvame do Bagdadu. Arabský matematik Al-Khwarizmi riešil kvadratické rovnice, čo zahŕňalo aj rátanie odmocnín. Rovnice riešil geometricky, ale aj algebraicky (používal čísla). Pre ľudstvo to bol dôležitý krok k symbolickej algebre (písmenkám a znamienkam).[19]

🌻 1202 AD - Európa sa pomaly znovu stavia na nohy. Grécke vedomosti, zachované a rozvinuté východnými národmi, prichádzajú na naše územie. Jedným z ľudí, ktorí ich prinášajú je Fibonnaci. Jeho zásluhou sa k nám dostali indické a arabské metódy na riešenie kvadratických rovníc.[20]

🤼 1545 AD - okolo tohto roku sa vedomosti posunuli zase o kúsok ďalej. No posun sprevádzala menšia dráma. Keďže v tej dobe nemali TikTok a nemohli sa pretekať, kto dá viac fancy challenge, súťažili aspoň v matematike. Skrátka v tej dobe matematici fungovali tak, že si dávali navzájom rôzne výzvy. Kto niečo objavil, nechával si to pre seba, aby to mohol vo vhodnej chvíli vytiahnuť a omráčiť protivníka.

V týchto podmienkach istý Gerolamo Cardano riešil kubické rovnice a chcel dospieť k nejakému všeobecnému riešeniu. Lenže nevedel vyriešiť určitý typ rovnice, no zistil, že jeho kolega Tartaglia to vedel. Cardano požiadal Tartagliu, aby mu tajomstvo prezradil. Tartaglia mu to nechcel povedať, no Cardano stále naliehal, tak nakoniec Tartaglia poľavil. Pod podmienkou, že o tom nikomu nepovie a nikdy to nezverejní, povedal Cardanovi svoj postup na riešenie daného typu rovníc.

Vďaka tomu Cardano dokončil svoju metódu na vyriešenie kubických rovníc každého druhu. Bol to úspech ako hrom a Cardana svrbel jazyk. Najradšej by to hneď oznámil celému svetu, ale nemohol, pretože ho viazal sľub daný Tartagliovi. Pri jednom výlete do Bologne sa však stalo niečo nečakané. Cardanov šikovný žiak Lodovico Ferrari si všimol zápisky istého Scipioneho del Ferra. V tých zápiskoch boli vyriešené presne tie rovnice, ktoré mali od Tartagliu. A tieto zápisky boli staršie, ako vedomosti získané od Tartagliu.

Cardano neváhal. Napísal knihu Ars Magna a v nej publikoval svoju všeobecnú metódu na riešenie kubických rovníc. Keď sa to Tartaglia dozvedel, bol od jedu celý bez seba, pretože si myslel, že Cardano porušil sľub. Chcel vyzvať Cardana na verejný matematický duel, no ten odmietol a na miesto seba poslal Ferrariho. Duel sa konal v Miláne. Debatovalo sa celý deň a pokračovalo by sa aj na druhý, lenže Ferrari Tartagliu zničil a ten z Milána ušiel.

Debata priniesla Ferrarimu a Cardanovi slávu a mnoho pracovných príležitostí. Hovorí sa, že Ars Magna bola začiatkom modernej matematiky. Tak ako Cardano vystúpal hore, tak Tartaglia padol dole. Po dueli už že vraj nemal veľa práce. Zomrel chudobný a zabudnutý. Prosím, venuj Tartagliovi tichú spomienku, pretože aj vďaka jeho vedomostiam môžeš teraz súťažiť v TikTok challengoch a nemusíš si ruinovať život matematickými duelmi.

Okrem toho Cardano priniesol na svet aj niečo iné. Pri výpočtoch mu pod druhými odmocninami začali vychádzať záporné čísla. Vtedy si s tým ešte nevedel dať rady, no dnes to poznáme ako imaginárnu časť komplexných čísiel.[21]

➖✖➖=➕ 1526-1572 AD - na scénu prichádza ďalší taliansky matematik, Rafael Bombelli. Vysvetlil komplexné čísla, ktoré vyšli z Cardanových vzorcov a objavil pravidlá, podľa ktorých sa bude s nimi pracovať. Okrem toho bol prvý Európan, ktorý povedal, že mínus krát mínus je plus.[22]

🆎 1540-1603 AD - do hry sa zamiešal aj Francois Vieté, pretože jeho symbolická notácia veľmi uľahčila prácu s odmocninami.

📐 1596-1650 AD - René Descartes spravil analytickú geometriu. Korene rovníc (odmocniny) sa dali vizualizovať v súradnicovom systéme. Zasa to pomohlo počítaniu s odmocninami a umožnilo to ľuďom trochu iný pohľad na ne. Okrem toho stál za pomenovaním imaginárnych čísiel. Imaginárnymi ich voláme vďaka nemu.[23]

🍎 1642-1727 AD - Keď Newton zrovna nevyspával v jabloňovom sade, tak sa trochu venoval aj matematike. Možno inšpirovaný babylonskou metódou, spravil postup na všeobecné nájdenie odmocniny. Postup už obsahoval aj žhavú novinku - derivácie. $$X_{n+1} = X_n - \frac{f(x_n)}{f\prime(x_n)}$$ 👨‍🏫 1648-1715 AD - Joseph Raphson zjednodušil Newtonovu metódu. Dokonca už bola dosť ľahká na to, aby sa dala vyučovať na školách.

🌟 1710-1761 AD - Thomas Simpson spopularizoval Newtonovu metódu.[24]

🧮 1707-1783 AD - Euler rozšíril hľadanie koreňov rovníc o ich hľadanie pre nekonečné polynómy. Čiže existujúce metódy vylepšil a viac zovšeobecnil.[25]

🤔 1736-1813 AD - Joseph Louis Lagrange ďalej rozširoval teóriu týkajúcu sa hľadania koreňov polynómov. Zaoberal sa nejakými permutáciami týchto koreňov. Výskum síce nedokončil, ale jeho práca predstavovala základ pre teóriu grúp, ktorej sa neskôr venovali ďalší matematici.[26]

🪐 19. storočie - v tomto storočí sa veľmi zužitkoval predchádzajúci výskum v matematike. Hľadanie odmocnín našlo svoje uplatnenie vo výskume vesmíru (pohyb nebeských telies), termodynamike, elektrike a potom aj v ďalšom výskume matematiky. Na rýchle výpočty odmocnín používali tabuľky a posúvacie pravítka.

💻 20. storočie - toto storočie sa nesie v duchu nástupu počítačov. Vyvíjajú sa rôzne algoritmy na rátanie odmocnín. Newton-Raphsonova metóda si však našla svoje miesto aj tu. Takže dnes, keď si do kalkulačky v mobile naťukáš dáku odmocninu, tak dosť pravdepodobne používaš postup, ktorý má svoje korene okolo roku 2000 pred naším letopočtom.[27]

To bude o mocninových funkciách už všetko. Ďakujeme, že si to vydržal čítať až sem 😊.

Zdroje