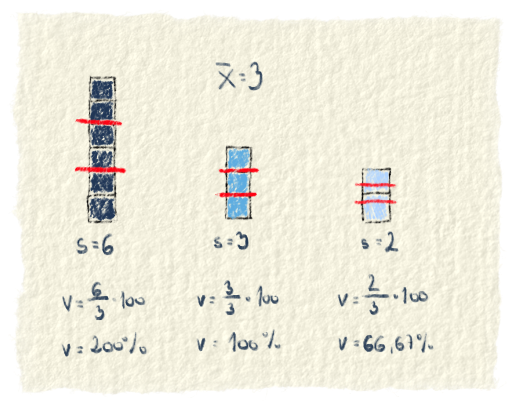Miery variability

Miery variability používame keď chceme vedieť ako veľmi sú údaje rozdielne. Ďalšie využitie je, keď je priemer viacerých štatistických súborov rovnaký a my ich chceme napriek tomu porovnať.

Tieto miery nám povedia niečo o tom, ako veľmi sa údaje od seba líšia. Väčšinou sa zisťuje, ako sú dáta rozložené okolo priemeru. Či sú ďaleko alebo blízko. Napríklad, ak máme dve čísla a ich priemer je 5, chceme vedieť, či sú obe blízko päťky (4 a 6: (4+6)/2=5) alebo sú ďaleko od päťky (-100 a 110: (-100+110)/2=5).

Čím sú údaje menej rozdielne, tým sú miery variability menšie. Či sú pre nás lepšie vyrovnané dáta alebo úplne rozdielne, záleží od problému, ktorí riešime.

Na obrázku ti chceme ukázať, čo znamená rozptýlenie dát okolo priemeru. Na prvej osi sú údaje okolo priemeru rozptýlené menej a na druhej viac. Údaje sú nakreslené bledomodré a priemer je číslo 5.

=Variabilita údajov — Obr. 1.: Prvé údaje sú od 4 po 6. Nejak veľmi sa od seba nelíšia, tak ich variabilita je menšia. Druhé dáta sú od 1 po 10. Ich údaje sa už líšia viac. Variabilita druhých dát je väčšia.

Variačné rozpätie

Variačné rozpätie hovorí o tom, v akom rozsahu sú dáta. Čím je menšie, tým sú dáta viac rovnaké. $$ R=x_{max}-x_{min}$$ Vzorec je ľahký. Je to rozdiel medzi najväčšou hodnotou a najmenšou hodnotu z dát.

Pre Inter Milano by sme zobrali najlepšieho Samira Handanoviča s 88 a najhoršieho Nicolò Barellu s 80. Vypočítali by sme to $ R=88-80=8$. Vieme, že Inter Milano má variačné rozpätie 8.

Priemerná absolútna odchýlka

Svoju funkcionalitu má priemerná absolútna odchýlka vo svojom názve. Že ako? No pozeraj. Najprv potrebujeme vypočítať priemer z dát. V priemernej absolútnej odchýlke sa pre každý údaj zisťuje rozdiel medzi ním a priemerom. To je tá odchýlka (že ako veľmi sa údaj líši od priemeru). Z rozdielov medzi údajmi a priemerom berieme absolútnu hodnotu. Je to preto, lebo chceme vedieť iba ten rozdiel, o koľko je údaj väčší alebo menší. Nechceme vedieť to, či je menší alebo väčší. To, že sa berie absolútna hodnota zastrešuje v názve slovo absolútna. Teraz to priemerná. Dobre, takže v tomto momente už máme niekde vyrátané rozdiely medzi údajmi a priemerom. Vieme povedať, o koľko sa asi údaje líšia od priemeru? No ťažko, lebo keď si to vyskúšaš na nejako príklade, tak uvidíš, že jeden rozdiel ti vyjde tak, druhý inak, tretí bude zasa iný. Potrebujeme z toho dostať iba jedno číslo. To spravíme tak, že z týchto rozdielov spravíme priemer. Dostaneme tak, že o koľko priemerne sa líšia údaje od priemeru, teda dostaneme priemernú absolútnu odchýlku. $$ \overline{d}=\frac{1}{n} \sum_{i=1}^n \left| \overline{x} - x_{i} \right| $$ Vzorec si rozoberieme zvnútra. V sume vidíš $ \left| \overline{x} - x_{i} \right| $, čo znamená že sa od priemeru odráta údaj a z rozdielu sa spraví absolútna hodnota. Znak $ \sum $ nám hovorí, že ideme spočítavať. Spočítava sa samozrejme to, čo je vnútri sumy. Zrátavajú sa teda absolútne hodnoty z rozdielu medzi priemerom a údajmi. Robí sa to pre každý údaj. Prezradiť ti to môžu aj písmenká i a n naspodku a navrchu sumy. Písmeno i hovorí, že odkiaľ sa začína spočítavať a písmeno n, že pokiaľ. V tomto vzorci vidíš, že sa berú údaje od prvého po posledný (po n). Rozdiely sú sčítané a teraz treba priemer dokončiť. Na to je ten zlomok $ \frac{1}{n} $, ktorý výsledok sumy vydelí počtom údajov. Dúfam, že si si už za svojho pôsobenia vo vzdelávacom systéme všimol, že keď niečo násobíš $ \frac{1}{n} $, tak to vlastne delíš n-kom.

Podobne, ako variačné rozpätie, aj priemerná absolútna odchýlka hovorí o tom, ako veľmi sú dáta rozptýlené okolo priemeru. Nie je to však už iba nejaké rýchlo vypočítateľné orientačné číslo, ale je to konkrétna hodnota. Priemerná absolútna odchýlka presne hovorí o tom, o koľko priemerne sa údaje líšia od priemeru.

Pre Inter Milano to vypočítame takto:

$$ \overline{d}=\frac{1}{11} \sum_{i=1}^{11} \left| \overline{overall} - overall_{i} \right| = 2,479 $$

V hlave budeš robiť klasický výpočet. Ak by si náhodou zabudol, tak zvislé zátvorky znamenajú absolútnu hodnotu. (|83.73-88| + |83.73-88| + |83.73-86| + |83.73-85| + |83.73-85| + |83.73-84| + |83.73-82| + |83.73-81| + |83.73-81| + |83.73-81| + |83.73-80|)/11 = 27.269 / 11 = 2.479. Teraz vieme, že hráči Interu Milano sa od priemeru líšia priemerne o 2,479 bodov overall.

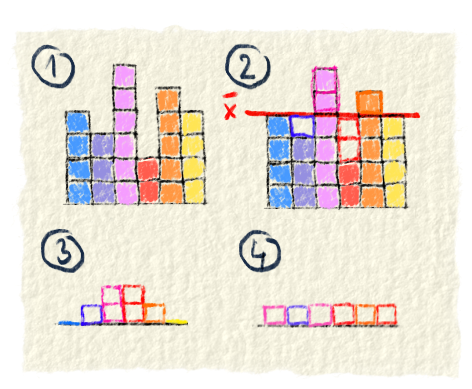
=Rátanie priemernej absolútnej odchýlky — Obr. 2.: Tu je ukázané, ako funguje matematika v priemernej absolútnej odchýlke. 1. Namerané údaje. 2. Pre každý údaj sa dozvieme, o koľko sa líši od priemeru. 3. Rozdiely medzi údajmi a priemerom. 4. Z rozdielov sa spraví priemer a vidíme, že údaje sa priemerne líšia od priemeru o jednu kocku.

Rozptyl

Niektoré údaje sa líšia od priemeru málo a iné veľa. V niektorých situáciách (napríklad, keď trénuješ neurónovú sieť :D ) treba veľký rozdiel zvýrazniť oveľa viac ako malý. Čím je rozdiel väčší, tým ho chceš viac zvýrazniť. Takúto vec ti spraví kvadratická funkcia. Ak nevieš čo to je, tak umocni rozdiel medzi priemerom a údajom na druhú a máš kvadratickú funkciu. Skús si umocniť zopár čísiel a uvidíš, že čím väčšie číslo, tým je výsledok o dosť väčší. Rozptyl sa ráta podobne ako priemerná absolútna chyba, ibaže z rozdielu medzi priemerom a údajom sa nerobí absolútna chyba, ale umocní sa na druhú.

Fajn, máme teda zvýraznené veľké rozdiely a keď treba vieme rozptyl použiť. Ale má to jednu chybičku na kráse a tá nám niekedy môže vadiť. Ukážeme ti to na príklade. Na telesnej dal učiteľ behať šesťdesiatku a každému žiakovi meral čas. Pretože ho bavila štatistika, vyrátal si rozptyl. No a tu je tá chybička na kráse. Keď niečo dávaš na druhú, tak výsledok je na druhú. Keď meriaš čas v sekundách a dáš ho na druhú, tak budeš mať sekundy na druhú. Chceme ti týmto ukázať, že rozptyl nevyjde v jednotkách údajov, ale v tých jednotkách na druhú. Niekedy ti to nevadí a potrebuješ práve vypočítať rozptyl. Ale sú situácie, keď chceš mať zvýraznené rozdiely a zároveň to mať v jednotkách údajov. O tom však neskôr, v smerodajnej odchýlke. $$ s^2=\frac{1}{n} \sum_{i=1}^n \left( \overline{x} - x_{i} \right)^2 $$ Vzorec je podobný ako v priemernej absolútnej odchýlke. Týmto $ \left( \overline{x} - x_{i} \right)^2 $ sa vypočítajú rozdiely medzi údajov a priemerom a každý z nich sa dá na druhú. Suma zabezpečí, že sa ich výsledky spočítajú a nakoniec sa to predelím n-kom, aby bol priemer. Funguje podobne ako priemerná absolútna odchýlka. Rozdiel je ten, sa z rozdielu medzi priemerom a údajom nerobí absolútna hodnota, ale výsledok sa umocní na druhú.

Pre Inter Milano to vypočítame takto:

$$ s^2=\frac{1}{11} \sum_{i=1}^{11} \left( \overline{overall} - overall_{i} \right)^2 = 7.652 $$

V hlave alebo na kalkulačke si sumu rozpíšeš normálne: ((83.73-88)² + (83.73-88)² + (83.73-86)² + (83.73-85)² + (83.73-85)² + (83.73-84)² + (83.73-82)² + (83.73-81)² + (83.73-81)² + (83.73-81)² + (83.73-80)²)/11 = 84.182 / 11 = 7.652. Ak sa ti nechce toto rátať z hlavy, tak môžeš aj na papier. Aspoň uvidíš, že zápis so sumou ušetrí veľa miesta.

Zvýraznenie väčších odchýlok ti ukážeme na príklade. Tu sú rozdiely medzi údajom a priemerom: 1,2,3,4,5,6. Absolútna hodnota je to isté. Druhé mocniny rozdielu medzi priemerom a údajom sú tieto: 1,4,9,16,25,36. Už tak na pohľad vidíš, že 1 a 6 nie sú až tak rozdielne čísla. Ale medzi 1 a 36 je oveľa väčší rozdiel. Druhá mocnina práve väčší rozdiel zvýrazní viac ako menší rozdiel.

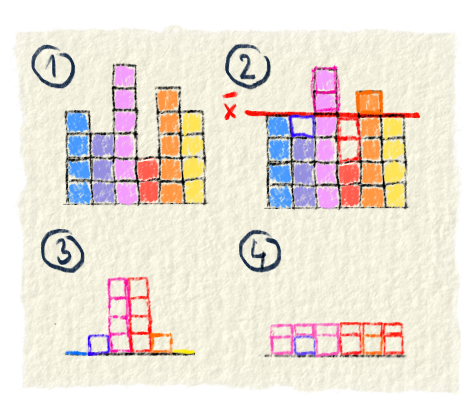
=Rátanie rozptylu — Obr. 3.: Tu je zobrazené, ako funguje matematika v rozptyle. 1. Namerané údaje. 2. Pre každý údaj sa dozvieme, o koľko sa líši od priemeru. 3. Rozdiely medzi údajmi a priemerom sa umocnia. Všimni si, že veľké rozdiely sú viac zvýraznené než pri priemernej absolútnej chybe. V našom príde je týmto veľkým rozdielom číslo 2. Kým pri priemernej absolútnej chybe je rozdiel stále dva, tak pri rozptyle je už štyri. 4. Z umocnených rozdielov sa spraví priemer. Priemer je 1,667 a s trochou fantázie si domysli na obrázku, že údaje sa priemerne líšia o 1,667 kocky (tá vrchná "kocka" je 0,667 kocky ).

Rozptyl môžeš nájsť aj pod názvom variancia alebo disperzia.

Smerodajná odchýlka

V rozptyle sme spomínali, že sa nám niekedy hodia zvýraznené veľké odchýlky, ale chceme ich mať v jednotách údajov. Nie je nič ľahšie. Rozptyl vyjde v jednotkách na druhú a keď mám niečo na druhú a už tu nechcem mať na druhú, tak to odmocním. Presne to robí smerodajná odchýlka. Odmocňuje rozptyl. Že tam tie veľké rozdiely zostali zachované si môžeš všimnúť na tom, že smerodajná odchýlka je trochu väčšia ako priemerná absolútna. Čím je väčšia od priemernej absolútnej, tým sú v údajoch väčšie rozdiely. Zároveň to už však je v jednotkách údajov a teraz môžeš povedať, že údaje sa priemerne líšia od priemeru o toľko a o toľko. $$ s=\sqrt{\frac{1}{n} \sum_{i=1}^n \left( \overline{x} - x_{i} \right)^2} $$ Vzorec je teda rovnaký ako rozptyl, len sa robí z neho druhá odmocnina.

Smerodajnú odchýlku pre Inter Milano vyrátame takto:

$$ s=\sqrt{\frac{1}{11} \sum_{i=1}^{11} \left( \overline{overall} - overall_{i} \right)^2} = 2.766 $$

Rozptyl pod odmocninou už máme vyrátaný, tak to len odmocníme $ s=\sqrt{7.652} = 2.766$. Teraz môžeme povedať, že hráči sa priemerne od seba líšia o 2,766 overall-u.

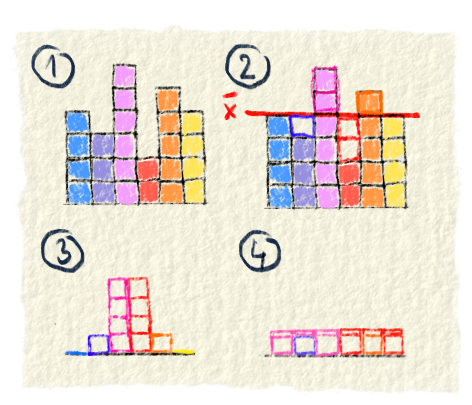
=Rátanie smerodajnej odchýlky — Obr. 4.: Tu je matematika skrývajúca sa za smerodajnou odchýlkou. 1. Namerané údaje. 2. Pre každý údaj sa dozvieme, o koľko sa líši od priemeru. 3. Rozdiely medzi údajmi a priemerom sa umocnia. Všimni si, že veľké rozdiely sú viac zvýraznené než pri priemernej absolútnej chybe. V našom príde je týmto veľkým rozdielom číslo 2. Kým pri priemernej absolútnej chybe je rozdiel stále dva, tak pri rozptyle je už štyri. 4. Z umocnených rozdielov sa spraví priemer a ten sa odmocní. Výsledok je 1,291 a s trochou fantázie si domysli na obrázku, že údaje sa priemerne líšia o 1,291 kocky (tá vrchná "kocka" je 0,291 kocky ).

Smerodajnú odchýlku môžeš nájsť aj pod menami štandardná odchýlka alebo štandardná deviácia.

Variačný koeficient

V živote človeka príde moment, keď bude chcieť porovnať variabilitu dvoch rôznych súborov. Aj keď sa to nezdá, ale dá sa to. Keď pozrieme na dáta, vieme povedať, že tieto sú okolo priemeru rozptýlené málo, tieto trochu viac a iné sú rozptýlené veľmi ďaleko.

Doteraz sme mali miery variability, ktoré sú absolútne. To znamená, že od ničoho nezávisia. Tieto miery vyjadrujú konkrétne číslo, ako veľká je variabilita. Oni sú fajn, lebo vieš povedať, že údaje sa od priemeru líšia o toľko a o toľko. Ale variabilita dvoch súborov sa pomocou nich porovnať nedá.

Predstav si, že si biológ a z nejakého dôvodu by si potreboval zistiť, či sa vo svojich veľkostiach viacej líšia baktérie alebo vráskavce obrovské. Zmeriaš si teda veľkosť niekoľkých baktérií a niekoľkých vráskavcov. Zistíš, že baktérie majú veľkosť pár stoviek nanometrov a vráskavce mávajú okolo 30 metrov. Z oboch vypočítaš smerodajnú odchýlku. Pre baktérie ti vyjde napríklad 100nm a pre vráskavce 1m. Aby sme neporovnávali metre a nanometre, premeníme si ich na centimetre. 100nm je 0,00001cm a 1m je 100cm. Je to jasné, vráskavce sa líšia vo svojich veľkostiach viac. Ale naozaj? Nehrá tu rolu aj veľkosť živočíchov? Asi to s tým porovnaním nebude také ľahké. Nemôžeme predsa takto porovnávať dve rozdielne veci.

Našťastie existuje spôsob, ako vyriešiť tento problém. Variabilitu údajov môžeme vyjadriť relatívne. Vyjadríme ju vzhľadom na veľkosť údajov, čiže zistíme, ako veľká časť variability pripadá na jednu jednotku údajov. Údaje sú v nejakých jednotkách. Keď meriaš veľkosť vráskavca, tak údaje a priemer, ktorý dostaneš bude v metroch. Veľkosť baktérií je v nanometroch. Ceny bytov sú v eurách. Telocvikár meria čas v sekundách. Futbalisti majú overall v bodoch. Jedna jednotka je teda 1 meter, 1 nanometer, 1 euro, 1 sekunda, 1 bod atď. Aká veľká časť variability pripadá na jednu jednotku údajov zistíš tak, že variabilitu vydelíš veľkosťou údajov. Ten, kto vymýšľal variačný koeficient si povedal, že na vyjadrenie variability použije smerodajnú odchýlku a na veľkosť údajov použije priemer. $$ v=\frac{s}{\overline{x}}*100 $$ Toto je teda variačný koeficient. Smerodajná odchýlka sa vydelí priemerom a dostaneme aká časť variability pripadá na jednu jednotku. Výsledok sa ešte môže (aj nemusí) vynásobiť stovkou a dostaneme variabilitu dát v percentách. Vďaka tomu vieme povedať, či je variabilita malá alebo veľká. Keď vyjde málo percent, tak dáta sú rozptýlené okolo priemeru málo a keď veľa percent, tak sú rozptýlené veľa.

Skúsme teda porovnať variabilitu vráskavca a baktérií variačným koeficientom. Vráskavec meria v priemere 30m a baktéria 400nm. Smerodajná odchýlka pre vráskavce je 1m a pre baktériu 100nm. Teraz to dokonca ani netreba premieňať na centimetre, lebo variačný koeficient je variabilita na jednu jednotku dát a je jedno, aká je tá jednotka. Je jedno či sú to metre, alebo nanometre alebo niečo iné. No poďme počítať. Variačný koeficient pre vráskavca je 1m/30m=0,033=3,33%. Variačný koeficient pre baktérie je 100nm/400nm=0,25=25%. Teraz je už jasné, že viac sa líši veľkosť baktérií ako veľkosť vráskavcov. O dosť viac. Takto môžeme porovnávať variabilitu údajov, ktoré nie sú rovnaké. Napríklad môžeme porovnať variabilitu teplôt v máji s variabilitou cien bytov alebo podobné hruška a jablká.

Pozrime sa na to, ako veľmi sú rozptýlení hráči Inter Milano. Vypočítame si variačný koeficient $ v=\frac{2,766}{\overline{83,73}}*100=3,303%$. Po výpočte vidíme, že hráči Interu nie sú veľmi rozptýlený. 3,303% nie je veľa. Dokonca ich môžeme porovnať s baktériami a vráskavcami. Veľkosť baktérií a počet bodov overall hráčov má zhruba rovnaké rozptýlenie.