Číselné množiny

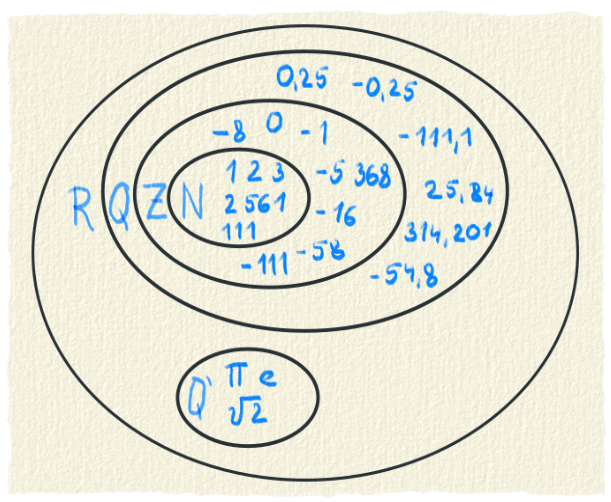
Čísla delíme do skupín, ktoré sa nazývajú množiny.

• Prirodzené čísla, ozn. N. Patria sem všetky celé čísla od 1 po nekonečno.
• Celé čísla, ozn. Z. Sú to všetky prirodzené čísla, záporné čísla a nula.
• Racionálne čísla, ozn. Q. Patria sem všetky čísla, ktoré sa dajú napísať v tvare zlomku, teda aj celé čísla.
• Iracionálne čísla. Sú to čísla, ktoré sa nedajú napísať v tvare zlomku. Patrí sem napríklad Pí. Ich označenie nie je jednoznačné, ale my budeme používať Q'. [1]
• Reálne čísla, ozn. R. Patria sem všetky racionálne a iracionálne čísla. Reálne čísla patria do množiny komplexných čísiel, ale o tom inokedy.

Ako vznikli číselné množiny

Na začiatku našich dejín ľudia nepotrebovali počítať, nemali žiadnu matematiku a bolo im dobre. Lenže potom sa začali rozvíjať, vykonávali čoraz náročnejšie činnosti a už začali potrebovať čísla.

Jeden z prvých dôkazov toho, že ľudia vedeli počítať je kosť Ishango [3]. Na kosti sú krátke zárezy, akoby paličky, ktoré označujú nejaký počet. Inde sa zase používali kúsky hliny až postupne sa vyvinuli čísla, ako ich poznáme dnes. Viac o vzniku čísiel si môžeš prečítať v článku Ako vznikli čísla.

Momentálne je pre nás dôležité, že ľudia vedeli určiť počet nejakých vecí. Na začiatku ľudstva viac ani nepotrebovali. Stačilo im vedieť, koľko členov má rodina (keď niekto chýbal, snáď ho išli hľadať), koľko chytili mamutov a že keď chytia ďalších budú mať viac a keď ich zjedia, budú mať menej. Čísla, ktoré prirodzene vyjadrovali počet boli prvé, s ktorými sa človek stretol.

Neskôr, keď už začali žiť vo väčších spoločenstvách museli začať riešiť aj záporné čísla. Napríklad taký Albert sa chcel oženiť a nevestinej rodine bolo treba odovzdať 200 oviec. Poznáš to aj sám. Mladý človek má hocičo, len nie majetok. Zopár oviec Albert mal, ale ostatné si musel požičať od kamarátov. Teraz už nemal žiadne svoje ovce a navyše nejaké bol aj dlžný. Takto nejako sa mohli zrodiť záporné čísla. Stále však vyjadrovali celok, s tým rozdielom, že sa už dalo povedať, že takýto počet človek vlastní alebo toľkoto mu chýba. Medzi celé čísla postupom pribudla aj nula, ale tá má samostatný príbeh, ktorý je napísaný kúsok ďalej.

Staroveký Egypt bola asi najrozvinutejšia civilizácia, aká dovtedy existovala. Obchodovali s cudzinou, stavali úžasné stavby, zaujímali sa o medicínu a astronómiu. So všetkými týmito činnosťami určite prišla potreba niečo rozdeliť na časti. Dôkazom toho je papyrus [4], kde je zaznamenané prvé použitie delenia na svete. Pri delení už nestačia celé čísla, lebo niečo môžeš rozdeliť na polovicu, na tretiny, štvrtiny atď. Odteraz už ľudia budú môcť používať desatinné čísla.

Keď sa Pythagoras hrajkal so svojou vetou, prišiel na to, že keď má trojuholník dve strany veľké 1, tak preponu nedokáže napísať zlomkom. Neexistujú také dve čísla, ktoré keď sa spolu vydelia, tak vyjde odmocnina z dvoch. Postupom času ľudia prišli na to, že odmocnina z dvoch nie je jediné číslo, ktoré sa nedá vyjadriť zlomkom. Okrem nej je to aj odmocnina z troch, pí, eulerovo číslo alebo konštanta pre zlatý rez. Približne v tomto období končí vývoj čísiel o ktorých sa bavíme. Ďalej už vymýšľali samé dobré veci, napr. komplexné čísla.

Názvy číselných množín

Ako sa matematika rozvíjala, potrebovali ľudia rozdeliť a pomenovať čísla. Rozdelenie priamo vyplýva z toho, ako sa čísla vyvíjali. Názvy číselných množín sú po latinsky [5], pretože dlhú dobu (hádam až po dnes) bol vedecký jazyk latinčina.

Začneme prirodzenými číslami. Tie vyjadrujú nejaký počet. Sú všetky celé čísla od 1 po nekonečno. Ich používanie je pre nás prirodzené, lebo si za nimi vieme ľahko predstaviť počet nejakých vecí. Podľa toho dostali aj svoj názov prirodzené čísla. Prvý krát sa názov naturales (z lat. prirodzené) objavil v roku 1484. Použil ho nejaký Francúz Chuquet, keď svojej postupnosti čísiel 1,2,3... dal názov progression naturelle. Prirodzené čísla svoj názov numerus naturales oficiálne dostali až v roku 1771, v jednom vedeckom článku o logaritmoch. Označujú sa písmenom N, ako naturales.

Ďalšie čísla, ktoré ľudia objavili boli celé čísla. Sú tu všetky čísla od mínus nekonečno po nekonečno, teda obsahujú všetky prirodzené čísla a ešte aj záporné čísla. Keďže stále vyjadrujú nejaký celok (aj keď záporný) dostali názov celé čísla, po latinsky numerus integri. Svoje pomenovanie dostali v roku 1571, keď ich použil Thomas Digges vo svojej práci A geometrical practise named Pantometria. Označené sú písmenom Z, z germánskeho slova "zahlen", čo znamená čísla [6].

Potom Egypťania vymysleli čísla, s ktorými sa delí. Keďže tieto čísla vyjadrujú pomer, dostali podľa toho aj meno numerus rationales. Ratio je po latinsky pomer, tak z toho. Prvá vážna zmienka o názve numerus rationales je z roku 1685 a použil ho angličan John Wallis. My latinský názov prekladáme ako racionálne čísla. Tieto čísla sa označujú písmenom Q, pretože písmeno R už skôr ukradli reálne čísla. Písmeno Q sa používa preto, lebo je prvé písmeno latinského slova qoutus, čo znamená kvocient (kvocient je číslo udávajúce pomer dvoch hodnôt).

Iracionálne čísla majú svoj pôvod v gréckom slove „arrhetos“, čo znamená nevysloviteľné [7]. Asi preto, lebo povedať číslo s nekonečným počtom desatinných miest trvá trochu dlho. Len pre zaujímavosť, dnes vieme číslo Pí s presnosťou na 31 biliónov desatinných miest.

Reálne čísla pomenoval René Descartes v roku 1637. Názov reálne dostali, že vraj podľa toho, že opisujú "hmatateľný" počet v našom svete [8]. To znamená, že si vieš predstaviť, že máš dve jablká, že nemáš dve jablká alebo, že máš polku jablka.

Nula

Nule venujeme zvlášť kapitolu, lebo je to číslo, ktorému ľudia dlho nerozumeli. Keď ľudia nemali nič, tak im to ani nenapadlo počítať. Veď keď nemáš nič, tak čoho máš vlastne nula? Máš nula áut alebo nula ponoriek alebo nula peňazí? Nula bola pre ľudí príliš abstraktné číslo.

Jej prvé začiatky boli medzi Sumermi, ktorí ju používali ako náhradu za cifry. Vtedy už používali pozičnú číselnú sústavu a keď chceli vyjadriť, že na danej pozícií cifra chýba, napísali tam nulu. Napríklad pri čísle 100 chýba cifra na pozícií jednotiek a desiatok. Oni ju písali ako dva malé kliny.

Ďalší významný míľnik v živote nuly prišiel niekedy v 7. storočí n.l.. Indický matematik Brahmagupta prišiel na to, že nula môže reprezentovať aj počet. Keď sa k niečomu pričíta alebo odčíta, tak sa to nezmení a keď sa odčíta číslo od samého seba, výsledok je nula.

O storočie neskôr Arabský matematik al Khowarizmi spravil symbol nuly tak, ako ho poznáme dnes. A až na začiatku druhého tisícročia sa nula dostala medzi ľudí, keď ju spopularizoval Fibonacci.

Ako počítajú zvieratá

Ľudia nie sú jediný, ktorí vedia počítať. Okrem nás existuje zopár šikovných hlavičiek aj medzi zvieratami. Niektorí sú dokonca dosť dobrí. Musia byť, pretože vedieť počítať je pre nich životne dôležité.

🐕 Psy: Ak si myslíš, že tvoj štvornohý kamoš bude v matematike génius, musíme ťa sklamať. Vlci vedia počítať celkom dobre, ale psy už nie. Skrotením prišli o svoje matematické bunky. Zistilo sa to tak, že výskumníci dali psom misky so žrádlom. V niektorých nebolo nič, v niektorých bolo viac jedla a v niektorých menej. Chlpáči ešte dokázali rozlíšiť, či v miske je alebo nie je žrádlo, ale už nedokázali rozlíšiť, v ktorej miske je ho viac.

🦁 Levy: Levy žijú v skupinách a bránia si svoje teritórium. Ak do ich územia príde cudzia svorka levov, domáci sa musia rozhodnúť, či si teritórium budú brániť alebo radšej zdrhnú. Ak je votrelcov menej, tak na nich zaútočia. Ak je ich viac utečú, lebo vedia, že po nerovnom boji by si ešte dlho zašívali kožuchy.

🐸 Žaby: Zistilo sa, že toto zeleno-skákavé stvorenie je celkom dobrý matematik. Dokáže totiž napočítať do 10. Keď si žabia slečna vyberá frajera, musí byť z jej druhu. Žiab je veľa druhov a počítanie im uľahčuje spoznať ten svoj. V kŕkaní samčekov je určitý počet „pulzov“. Samička vie spočítať, koľko „pulzov“ je vo fešákovom kŕkaní a to jej pomôže odhaliť, či je žabiak z rovnakého rodu. Žabiaka vie odlíšiť aj dĺžka a hlasitosť kŕkania.

⬛🐦Vrany: Šikovné matematičky sú aj vrany. Dokážu určiť presný počet vecí. Robili s nimi také pokusy, že im ukázali tablet, kde bolo zobrazené určité množstvo nejakých vecí. Potom im ukázali viacero tabletov a na jednom z nich bolo rovnaké množstvo, ale iných vecí. Vrany si vybrali tablet s rovnakým množstvom, aj keď objekty boli iné.

🐦 Vták robin: Na Novom Zélande žije vtáčik podobný nášmu vrabcovi a volá sa robin. Ten vie počítať tak dobre, že sa ani nedá oklamať. Ukázali mu nejaký počet červíkov, a on si myslel, že ich dostane všetkých. Ale nedostal, dali mu menej. Robin na to prišiel a hodnú chvíľu sa tváril urazene.

🐎 Kôň Hans: Pán Wilhelm von Osten žil v 19. storočí, býval v Nemecku a bol učiteľ na dôchodku. Doma sa už strašne nudil, tak si vymyslel, že naučí svojho koňa Hansa počítať. Kôň mal matematický talent a zakrátko sa naučil sčítavať, odčítavať, násobiť a dokonca aj deliť. Svoje odpovede dával svetu na známosť tak, že zahrabal nohou.

🦜 Papagáj Alex: Irene Pepperberg mala papagája menom Alex. Irene učila papagája asi 10 rokov, ale vyplatilo sa to. Naučil sa veci, o ktorých sa myslelo, že vtáci nikdy nedokážu. Rozumel reči, vedel rátať, trochu čítať a Irene ho naučila niečo, čo majú len ľudia. Alex si dokázal uvedomiť sám seba. Vráťme sa však k matematike. Irene zobrala päť zelených kociek, šesť zelených loptičiek, štyri ružové loptičky a tri ružové kocky. Potom sa spýtala papagája, že koľko je ružových loptičiek. Alex odpovedal, že štyri. V tejto úlohe musel Alex zvládnuť viacero vecí. Musel si uvedomiť, že sa pýtajú práve jeho, musel porozumieť tomu, čo sa ho pýtajú. Musel vedieť rozlíšiť farby, tvary a musel ich vedieť spočítať.

🐒 Šimpanz Ai: Ai je samička šimpanza, ktorú vychoval istý japonský vedec. Už sme tu mali zvieratá, ktoré vedeli rozlíšiť počet nejakých vecí. Ai zašla ešte kúsok ďalej. Naučila sa číslice a vedela k nim priradiť počet. Je to úctyhodné hlavne preto, lebo vedela k niečomu abstraktnému, ako je číslica priradiť konkrétny počet. Iná vec je, keď fyzicky vidíš päť orechov, a iná, keď vidíš iba číslicu a máš si za ňou predstaviť päť vecí.[2]

Zdroje