História funkcií

Funkcia je zobrazenie, ktoré každému prvku x z množiny A priradí práve jeden prvok y z množiny B, pričom platí, že A ≠ ∅ a B ≠ ∅ Takto nejak znie definícia funkcie dnes. No kým sme sa ako ľudstvo k niečomu takémuto dopracovali, pretieklo veľa vody v potokoch.

pred 1350 AD - ešte nič

Z dnešného pohľadu by sa dalo povedať, že už starovekí Babylončania poznali niečo ako funkcie. Mali tabuľky, v ktorých boli zapísané čísla a pre každé číslo jeho druhá mocnina. Alebo naopak. Mali tabuľky s mocninami a pre každú mocninu bola zapísaná odmocnina. No oni vôbec nad týmto nerozmýšľali ako nad funkciou. Boli to pre nich iba tabuľky, kde si pohľadali potrebné údaje.

1350 AD - niektoré veci medzi sebou súvisia

Prvé náznaky funkcie datujeme zhruba od roku 1350 AD. Tu však ešte vôbec nemôžeme používať termín funkcia. Nič také neexistovalo a objaví sa až o nejakých 300 rokov neskôr. V tomto roku istý pán Oresme pozoroval prírodu a študoval jej zákony. Zdalo sa mu, že niektoré veci/veličiny sa menia na základe iných. Táto jeho myšlienka sa stane jedným zo základných pilierov niečoho, čo dnes voláme funkcia.

16., 17. storočie - matematické piliere sa stavajú

Letmú spomienku by sme mali venovať aj Vietému, ktorý v 16.-tom storočí priniesol do matematiky písmenká a umožnil tak nad vecami rozmýšľať oveľa abstraktnejšie.

Posunieme sa do roku 1640. V týchto časoch žil Galileo Galilei. Študoval tie svoje planéty, a pri skúmaní ich pohybu potvrdil Oresmeho myšlienku, že niektoré veci skutočne závisia na iných. Okrem toho spravil ešte jeden dielik, ktorý neskôr pomohol vystavať funkcie.

Zistil, že niektoré čísla sa nejakým spôsobom dajú namapovať/spojiť na iné/s inými. Napríklad takto pospájal kladné celé čísla a ich mocniny. No spravil aj zložitejšie mapovanie, ktoré je vysvetlené na obrázku nižšie:

Kým Galileo študoval planéty, na svet prišiel ďalší kúsok budúcej skladačky. René Descartes priviedol na svet analytickú geometriu. Jednalo sa o to, že geometrické útvary a rôzne krivky sa dali vyjadriť pomocou rovníc. Ukázalo sa, že keď je krivka vyjadrená rovnicou s dvomi premennými, tak tieto premenné medzi sebou súvisia.

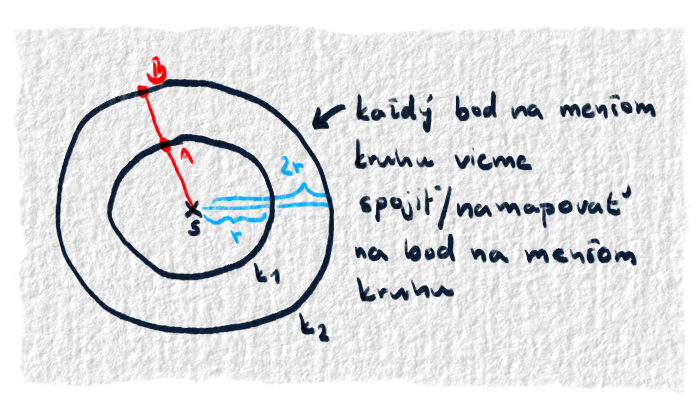
Ku koncu 17.-teho storočia si dvaja vedci, Leibniz a Bernoulli, písali listy. Dátum 1673 je pre funkcie dôležitý. Doteraz všetky vynálezy (závislosť premenných, písmenká, mapovanie, analytická geometria) sa udiali bez toho, aby autori chceli prispieť do nejakých funkcií. Oni skrátka robili niečo iné. Teraz sa však všetko začne spájať. Pretože v roku 1673 napísal Leibniz list Bernoullimu, v ktorom prvý krát použil slovo funkcia. Pomenoval ním závislosť nejakých geometrických veličín na tvare nejakej krivky. V jeho listoch prišli na svet aj výrazy ako konštanta, premenná a parameter.

Bernoulli zase napísal Leibnizovi, že funkcia je veličina vytvorená z iných premenných a aj konštantných veličín. Tiež funkciu spomenul v súvislosti so súradnicovým systémom.

18. 19. storočie - prvá definícia a veľký bordel

V roku 1748 sa vďaka Eulerovi funkcia stáva pevnou súčasťou matematiky a nie je len hmlistou myšlienkou. Taký malý spoiler k vývoju funkcií: v tomto roku vývoj funkcie určite neprestal. Naopak, naberá na obrátkach, pretože na najbližších cca 170 rokov budú mať matematici vo funkciách poriadny bordel.

V tomto roku (1748) napísal Euler slávnu knihu Introductio in analysin infinitorum. V tejto knihe sa Euler zaoberal matematickou analýzou, a teda aj funkciami. Povedal, že funkcia je analytický výraz. Síce už nepovedal, že čo to ten analytický výraz je, ale nevadí. Vo všeobecnosti sa to chápalo ako niečo zložené z čísiel a operácií (plus, mínus, krát, delené, mocnina, odmocnina...).

Okrem prvej vážnej definície funkcie sa Euler zaslúžil aj o to, že sínus, kosínus, tangens a ich bratia sa začali používať ako funkcie a nie sú to už len nejaké veci týkajúce sa kriviek a kruhu.

To, že Euler zadefinoval funkciu bolo síce milé, ale spravil to zle. Vďaka jeho definícii bola funkcia to isté, čo jej zápis pomocou analytického výrazu. To po celé 18. storočie robilo v matematike zmätky, ak nie rovno bordel. Lebo rovnaká funkcia mohla byť definovaná viacerými výrazmi.

Nasledujúcich 200 rokov preletíme rýchlo, pretože čítať to, je skôr na škodu veci ako na úžitok. Jednalo sa o to, že skoro každý matematik prišiel s trochu inou definíciou funkcie. Ďalší zas našli nejaké chyby v tých definíciách, ale opravili to ešte horšie ako to bolo. Pomaly sa to však utriasalo a veci sa stávali čoraz jasnejšími.[1]

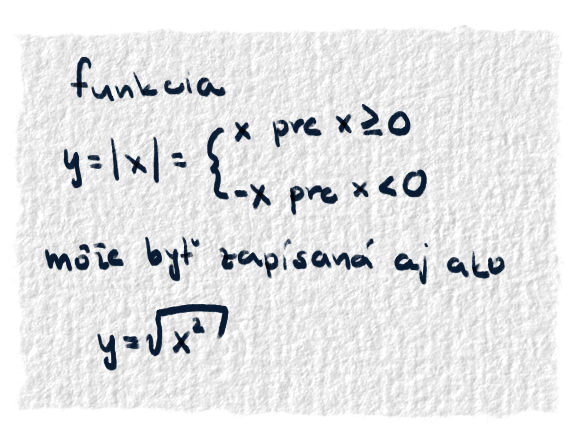
20. storočie - hurá, máme funkcie

Až napokon v roku 1923 spravil Goursat definíciu takú, akú ju poznáme dnes:

Funkcia je zobrazenie, ktoré každému prvku x z množiny A priradí práve jeden prvok y z množiny B, pričom platí, že A ≠ ∅ a B ≠ ∅

Zdroje