Goniometrické funkcie

Ľudia ako Newton, Descartes, Pascal, Fermat a mnohý ďalší spravili v matematike kus dobrej práce. Vďaka nim bola matematika v 18. storočí veda, ktorú sa oplatilo skúmať. Medzi ľudí, ktorí študovali matematiku, patril aj Leonard Euler. Okrem iného sa zaoberal aj matematickou analýzou, popri ktorej sa dostal ku goniometrii.

Vo svojej knihe Introductio in analysin infinitorum vyslovil myšlienku, že sínus a kosínus sa môžu používať ako funkcie. Nemusia to byť iba pomery strán v pravouhlom trojuholníku.

Čo znamená, že sa budú používať ako funkcie? To znamená, že im dáme nejaké číslo, oni s ním niečo spravia a vrátia výsledok. Oni sa vlastne správajú ako funkcie už sami o sebe. Dá sa im uhol a oni preň vrátia prislúchajúci pomer strán.

Ibaže je tu malý problém. Do sínusu a kosínusu sa môžu dať iba uhly menšie ako 90°, pretože väčšie v pravouhlom trojuholníku skrátka nie sú. Lenže keď už to chceme používať ako funkcie, chceme tam dať aj iné čísla. Chceme vedieť výsledky aj pre čísla väčšie ako 90° alebo menšie ako 0°, napr. pre 512°. Takéto uhly však v pravouhlom trojuholníku nenájdeme.

Výsledok treba dostať iným spôsobom. Potrebujeme niečo, kde by uhol mohol byť hocijaký a zároveň tam platilo, že sú to pomery strán v pravouhlom trojuholníku.

Pán Euler prišiel na to, že to niečo je jednotková kružnica. Dajú sa tam nakresliť pravouhlé trojuholníky, takže sa môžu vypočítať pomery strán. Veľkou pomocou je, že jedna strana trojuholníka môže mať dĺžku 1. Dôvod si povieme v článkoch o konkrétnych funkciách.

Keď si vypočítame pomery strán v týchto trojuholníkoch, dostaneme hodnoty goniometrických funkcii. Vieme ich zakresliť pomocou čiar. Teraz nie je dôležité, ako presne vznikli čiary, povieme si o tom neskôr. Hlavná myšlienka je, že hodnoty goniometrických funkcii sa dajú vyjadriť pomocou určitých čiar na jednotkovej kružnici. V obrázku sú vyznačené farebne.

Fajn, máme pravouhlé trojuholníky, ale ešte treba, aby sa do goniometrickej funkcie mohol dať hocijaký uhol. No a to sa dá veľmi ľahko. Uhol medzi "polomerom" a kladnou časťou osi x sa dá ľubovoľne meniť. Spolu s ním sa menia aj dĺžky čiar, teda hodnoty goniometrických funkcií.

Pomery strán pravouhlých trojuholníkov sme si zatiaľ ukázali iba v prvom kvadrante jednotkovej kružnice. Ako je to s ostatnými? Vo všetkých štyroch kvadrantoch sa dajú zostrojiť pravouhlé trojuholníky a následne vypočítať ich pomery strán. Samozrejme ich vieme zobraziť ako dĺžky jednotlivých čiar.

Ten uhol, pre ktorý sa počítajú pomery strán je medzi "polomerom" a tou "bližšou" časťou osi x. Na obrázku je pomenovaný písmeno β. Nás zaujíma uhol medzi "polomerom" a kladnou časťou osi x. Na obrázku je vyznačený písmenom α. Keďže dĺžky čiar sú pre α aj β rovnaké, z tohto pohľadu je jedno, ktorý uhol do funkcie dáme. Dávame však uhol α, lebo ten môže byť hocijako veľký.

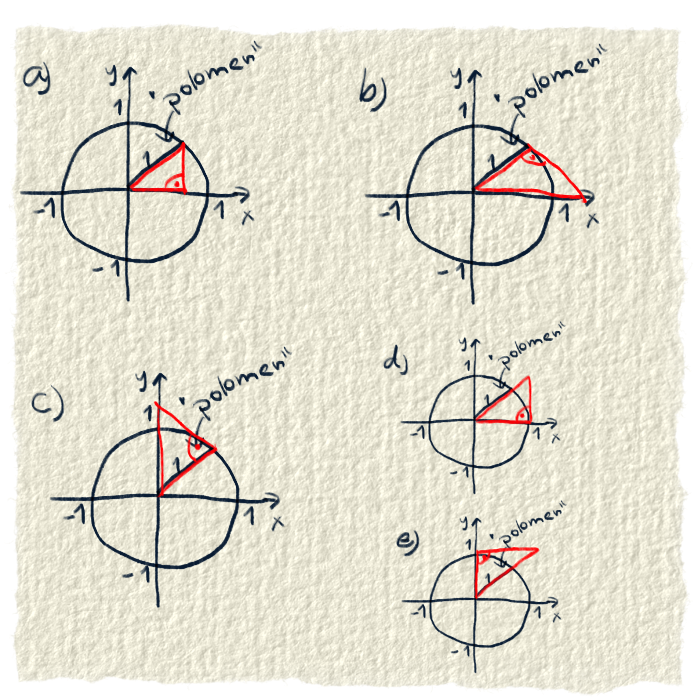
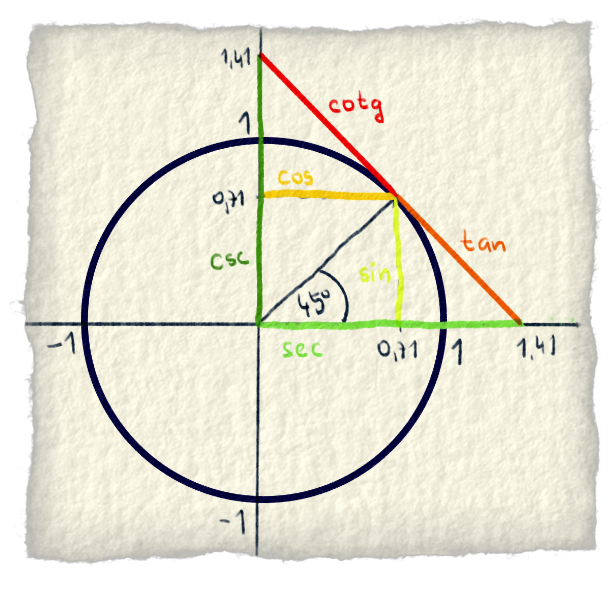
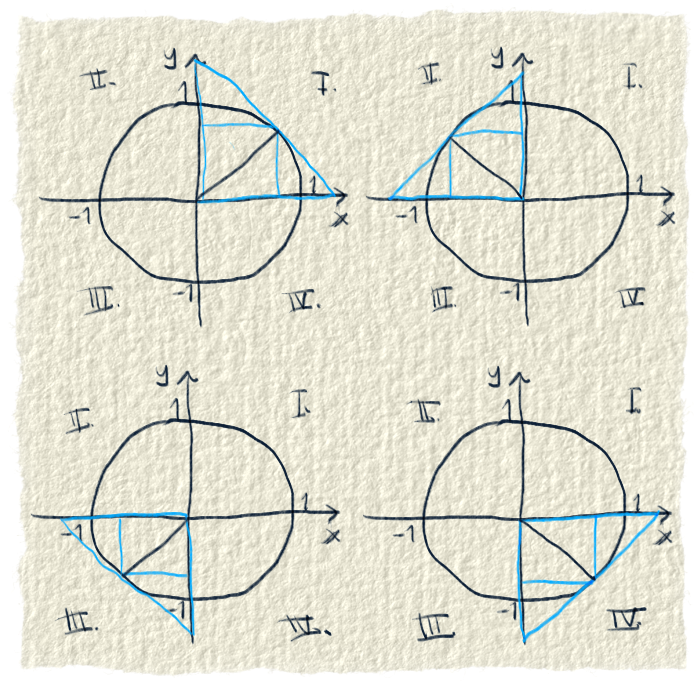
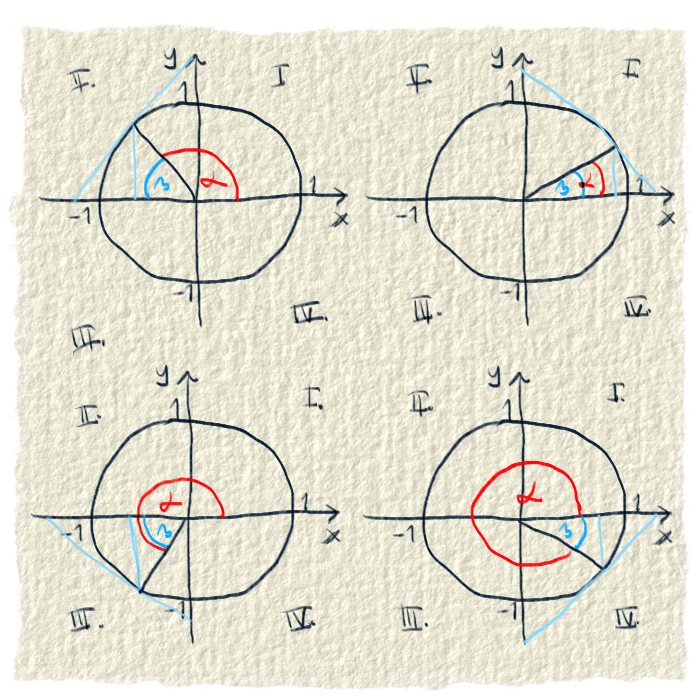
Vizualizácia goniometrických funkcií

Poznáme tri zaužívané spôsoby zobrazovania goniometrických funkcií. Jeden je na jednotkovej kružnici, druhý v grafe a tretí pomocou tabuľky. Na jednotkovej kružnici sú pekne vidieť vzťahy medzi funkciami, ale už horšie sú viditeľné vlastnosti funkcií. S grafom je to naopak. Lepšie sú vidno vlastnosti funkcií, ale horšie sú vidno ich vzájomné vzťahy. V tabuľke zasa ani nie je poriadne vidieť, že je to goniometrická funkcia, ale zato tam vieme vyrátať presné hodnoty funkcií.

Goniometrické funkcie

Goniometrické funkcie sú vysvetlené v zvlášť článkoch, pretože jeden článok by bol príliš dlhý. Tri najznámejšie a najpoužívanejšie - sínus, kosínus a tangens sú tu. Ich menej známy bratranci kotangens, sekans a kosekans sú tu.

Zdroje