Lineárna funkcia

Funkcie boli vymyslené na to, aby opisovali ako sa nejaké veci menia na základe iných. Napríklad ako sa dávka lieku mení na základe váhy pacienta. Alebo ako veľkosť úrody závisí od slnka, dažďa a živín v pôde. Príkladom funkcie je aj to, ako veľkosť povrchu gule závisí od jej polomeru.

Vzťah, ktorý opisuje lineárna funkcia patrí medzi najzrozumiteľnejšie pre nás ľudí. Hovorí o veciach, ktoré sa menia stále rovnako. Bežne sa vyskytuje vo svete okolo nás. Príkladom môže byť, ako sa prejdená dráha mení na základe rýchlosti, či ako sa mení počet zákuskov od počtu hostí alebo suma na účte na základe toho, koľko si tam človek odkladá.

Zmena medzi jednotlivými "krokmi" je vždy rovnaká. Napríklad ak auto prejde za 1 hodinu 60 kilometrov, tak aj za druhú hodinu prejde 60 kilometrov. 60 kilometrov prejde aj za tretiu, štvrtú, piatu hodinu. Skratka vždy prejde rovnako. Podobne, ak napríklad na svadbe sa ráta na jedného hosťa 5 zákuskov, tak na dvoch hostí sa už ráta 10, na troch sa ráta 15, na 100 hostí sa ráta 500 zákuskov.

História lineárnej funkcie

To čo sa vyvinulo do dnešnej lineárnej funkcie má korene dávno, pradávno. Ešte v starovekom Egypte riešili problémy, že koľko jačmeňa majú nachystať na výrobu x sudov piva, keď na jeden ide toľko a toľko kilogramov. Alebo koľko chlebov treba napiecť chlapom na stavbe, keď ich je tam x a každý z nich zje napr. 10 za deň (Egypťania mali menšie chleby ako my. Teda možno 😀).

Egypťania mali spôsob, ako vyriešiť problém, ktorý my dnes zapíšeme lineárnou rovnicou o jednej neznámej. Babylončania to updatli na dve rovnice o dvoch neznámych. Gréci spravili rovno upgrade a poskytli geometrické riešenie, ktoré zvládlo vyriešiť tieto problémy s ľubovoľným počtom neznámych.

Do svetového úsilia sa zapojili aj India, Čína či Araby. No významnejší posun nastal až od 17. stor., kedy sa vymyslela analytická geometria, na jej základe spravili v 18. stor. kalkulus a nakoniec to v 19. stor. sformalizovali. Dnes vďaka niekoľko tisícročnému úsiliu celého ľudstva, vieme zapísať lineárne problémy takýmto zápisom: $$ f(x) = ax+b $$ Viac detailov o histórii funkcií nájdeš tu.

Lineárna funkcia

Problémy, ktoré dnes voláme lineárne, existovali už pradávno. Opisujú veci, ktoré sa menia stále rovnako a v svete okolo nás sa vyskytujú viac než bežne. Bolo ich veľmi veľa a ľuďom sa nechcelo riešiť každý problém zvlášť. Potrebovali vymyslieť nejaký nástroj, ktorý ich bude schopný opísať všetky naraz. Riešením tejto situácie pomaly dospeli k lineárnej funkcii tak, ako ju poznáme dnes: $$ f(x) = ax+b $$ Pri vysvetľovaní jednotlivých členov funkcie si pomôžeme príkladom šetrenia peňazí. Predstav si, že máš účet, na ktorý každý mesiac odkladáš peniaze. Vďaka lineárnej funkcii si vieš vyrátať, koľko peňazí máš/budeš mať na účte v nejaký daný mesiac (aj bez toho, aby si vedel, že to čo robíš, sa nazýva lineárna funkcia).

f(x) - závislá premenná. Je to výsledok funkcie. V našom prípade je to našetrená suma. Táto suma závisí na tom, koľko mesiacov si budeš šetriť.

x - nezávislá premenná. Za ňu sa dosádzajú čísla. V našom prípade sa sem dosadí počet mesiacov šetrenia. To, koľko mesiacov šetríš nezávisí na ničom. Sporiť môžeš ľubovoľný počet mesiacov.

a,b - koeficienty lineárnej funkcie. Sú známe. Sú to tie čísla, ktoré vidíš, keď máš zadanú nejakú lineárnu funkciu. K nim sa dostaneme o chvíľu.

Lineárna funkcia opisuje veci, ktoré sa menia stále rovnako. Tá zmena sa nijak nemení.

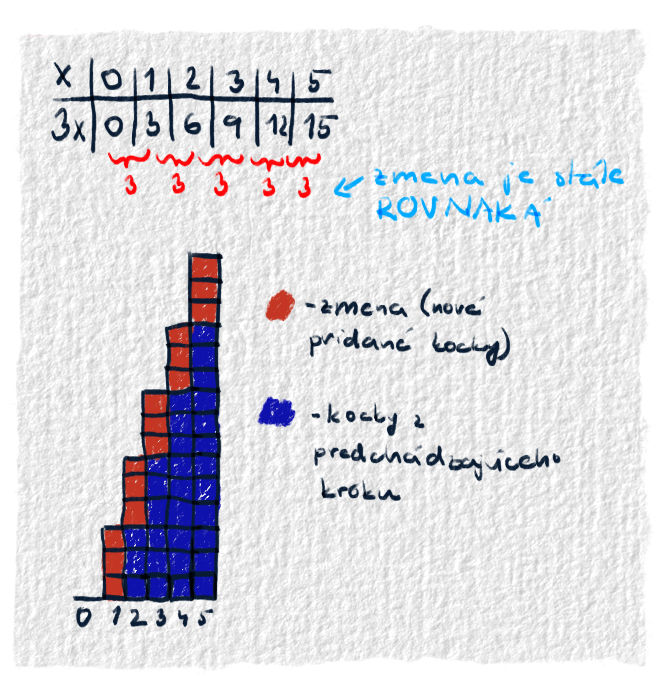
Koeficienty lineárnej funkcie

Koeficienty a a b opisujú veľkosť zmeny a počiatočný stav veličiny.

Ako vyrátaš, koľko peňazí už máš našetrených? No dáš počet mesiacov krát suma, ktorú šetríš. Suma je stále rovnaká, to čo sa mení je počet mesiacov. Lebo chceš vedieť, koľko budeš mať našetrené napríklad po mesiaci, 10-tich mesiacoch, po 5 rokoch. Ak šetríš 12 mesiacov po 50 eur, tak na účte bude 50*12=600 eur. Ak šetríš 24 mesiacov, tak suma na účte bude 50*24=1 200 eur. No môžeš šetriť aj viac alebo menej. Môžeš šetriť napríklad iba 2 eurá alebo 1000 eur. Vo všeobecnosti túto veľkosť zmeny označujeme písmenkom a. $$ f(x) = ax $$ V našom prípade sa teda pod a bude skrývať suma, ktorú si každý mesiac odložíš. Čím viac si budeš odkladať, tým rýchlejšie bude suma na účte rásť. No nemusíš si iba odkladať. Môžeš si z účtu vyberať. Pôjdeš síce do dlhu, ale ak sa ti páči bývanie pod šírim nebom (resp. pod mostom), tak to nevadí. Týmto sme chceli povedať, že veličina nemusí iba rásť, ale môže aj klesať. V takom prípade sa bude pod a skrývať záporné číslo.

Druhým koeficientom je písmeno b. Reprezentuje akýsi počiatočný stav veličiny. Predstav si, že šetríš, ale nezačínaš na nule. Rodičia ti dajú do začiatku nejakú tú stovku. Vtedy svoj stav účtu zistíš ako počet mesiacov šetrenia krát výška odkladanej sumy plus vklad od rodičov. Či si budeš výšku konta zisťovať pre mesiac šetrenia, pre 5 mesiacov alebo pre 50 mesiacov, ten vklad od rodičov je stále rovnaký a teda ho iba pripočítaš k zistenej sume. Vo všeobecnosti sa vo funkcii prirátava nejaké číslo, skryté za písmenko b: $$ f(x) = ax+b $$ Samozrejme začínať sa nemusí iba v pluse. Ak ti rodičia nič nedajú a ty navyše rozbiješ okno na školskej jedálni, tak si nielen v kaši ale aj v mínuse, pretože okno musíš zaplatiť. Vtedy musíš sumu za okno odrátať od našetrenej sumy a teda pod písmenom b bude záporné číslo.

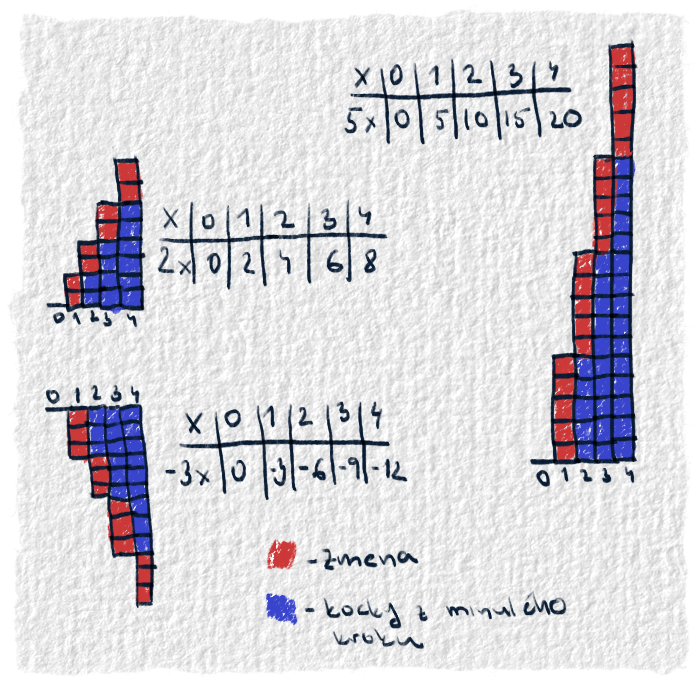
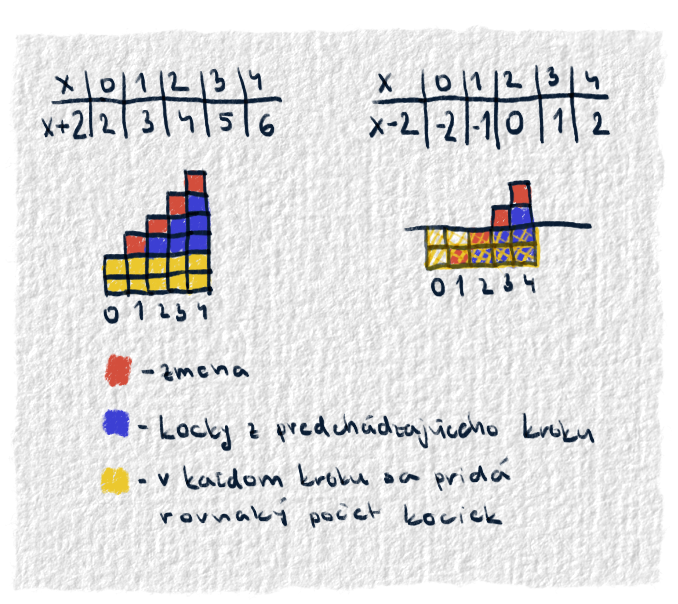
Graf lineárnej funkcie

Účinok koeficientov na funkciu si vysvetlíme tu.

Koeficient a hovorí o tom, ako veľká je zmena. Teda ako veľa peňazí odkladáme. Čím väčšie bude a, tým strmší bude graf, pretože susedné hodnoty sa budú od seba viac líšiť. Keď je zmena záporná, tak graf bude klesať, pretože výsledky funkcie sa budú postupne zmenšovať. Aj tu platí, že čím sa bude viac uberať, tým graf pôjde strmšie nadol (lebo susedné hodnoty sa budú líšiť viac a viac).

Koeficient b posúva graf hore a dole po y osi. Reprezentuje nejaký počiatočný stav veličiny, ktorý sa nemení. Napríklad Jožko, Terezka a Ferko si chcú šetriť, ale začínajú v úplne iných podmienkach. Jožko 20 eur našiel, Ferko 20 eur stratil a Terezka nič nenašla a ani nič nestratila.

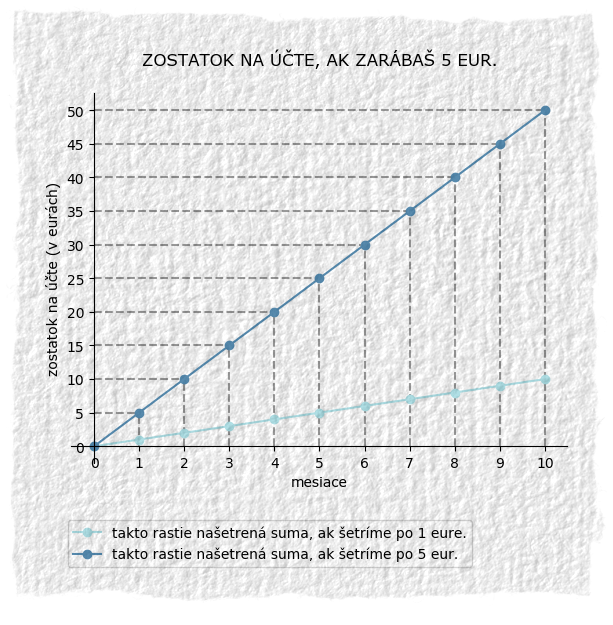
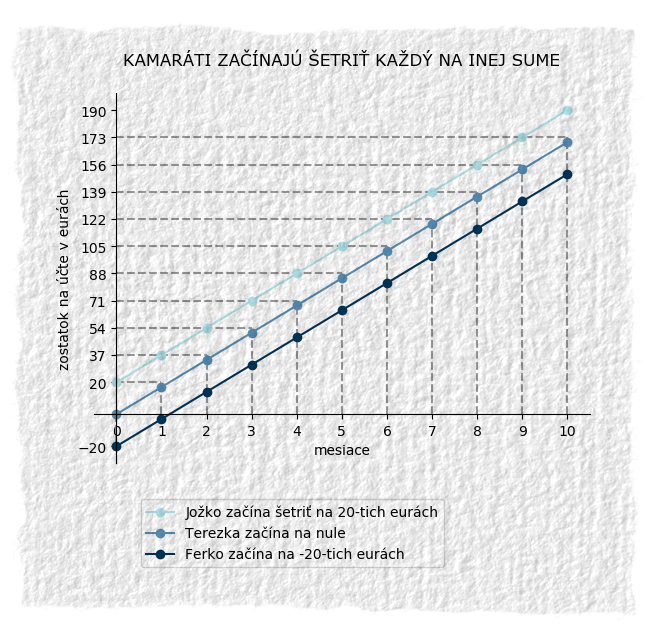
Keby chceme pre nich nakresliť graf, tak Jožkov bude posunutý nahor, lebo vždy sa mu k našetrenej sume pripočíta 20 eur. Ferkov bude posunutý nadol, lebo on bude mať vždy o 20 eur menej. Terezkin graf nebude posunutý nijak, lebo k jej našetrenej sume sa nič nepričíta ani neodčíta.

Keby ťa náhodou lineárna funkcia strašne moc bavila, tak tu prikladáme ešte link na náš starší článok: Lineárna funkcia