Použitie analytickej geometrie v počítačovej grafike

Niekde na začiatku sme spomínali využitie analytickej geometrie. Rozobrali sme ho len tak letmo, že sa používa tam a tam. Tu máme pre teba konkrétny príklad, s ktorým sa stretávaš skoro každý deň a ani o tom nevieš. Analytická geometria sa totiž využíva v počítačovej grafike, ktorej súčasťou sú aj animované filmy a počítačové hry. Bez nej by to vlastne ani nemohlo existovať.

Analytická geometria sa samozrejme využíva aj vo veľa iných odvetviach, ale chceme ti ju ukázať práve na hrách, pretože sa s nimi stretávaš dosť často a možno si si niekedy položil otázku, že ako to celé funguje.

Najprv ťa zavedieme do sveta tvorcov počítačových hier, aby sme ti ukázali ako to celé vzniká. Ukážeme si aj nejaké základné veci, ktoré musíš vedieť o počítačoch. Nakoniec sa pustíme do matematiky, ktorá tvorí základ hier.

Ako vzniká hra

Na samom začiatku stojí myšlienka. Ak ideš robiť hru, musíš vedieť, o čom tá hra bude. My budeme v tomto článku robiť hru o Červenej čiapočke. Bude to úplný trhák.

Keď už vieš, o čom bude hra, musíš si spraviť prieskum trhu. To znamená, že si pozrieš podobné hry, aby si videl, či už náhodou taká hra nie je. Prípadne sa môžeš aj inšpirovať, ale musíš sa držať hesla „steal like king, not like thief“.

Zistil si, že tvoja hra bude unikát (v skutočnosti nebude, lebo dnes je vymyslené už hádam všetko) a môžeš sa pustiť do hry. Do tímu musíš pribrať grafika a programátora. Jeden ti spraví objekty a grafiku do hry a druhý zaručí, že hra bude fungovať. Ak si šikovný, netreba ti ani jeden, lebo si spravíš všetko sám. Aj tak sú drahí.

Nakoniec hru otestuješ. Dáš ju zahrať kamarátom, rodine alebo profesionálnym testerom. Spýtaš sa ich, či sa im hra páčila, čo by na nej zmenili a podobne. Spätná väzba od používateľov je dôležitá. Koniec koncov hra je určená pre nich. Ak ti testeri našli veľa chýb, musíš hru opraviť.

Hra je otestovaná, funguje bez problémov. Už ju len zavesíš do nejakého online obchodu a užívaš si zarobené milióny.

Čo všetko musíš vedieť o počítačoch

Cesta od myšlienky k miliónom na účte samozrejme nie je taká jednoduchá. Okrem dobrej myšlienky musíš vedieť zopár vecí o počítačoch, trochu o fyzike, niečo z matematiky a vlastne tak skoro zo všetkého.

Všetky objekty, ktoré budeš používať v hre, musíš nejako dostať do počítača, musíš ich tam mať uložené, treba ich zobraziť a možno aj nejako rozhýbať. V našej hre budeme používať Červenú čiapočku, babičku, vlka, poľovníka, domček a posteľ pre babičku, košíček s dobrotami a tmavý hustý les.

Teraz si ideme vysvetliť použitie analytickej geometrie vo vyššie spomenutých krokoch. Popritom si vysvetlíme aj potrebné veci z počítačov a z fyziky.

Súradnicová sústava

Všetky objekty, ktoré budeme používať v hre, treba nejako dostať do počítača a držať ich tam uložené. Počítač rozumie len číslam, a preto treba všetky objekty premeniť na čísla. Tu prichádza na scénu súradnicová sústava.

Pomocou nej dokážeme všetky objekty zapísať pomocou čísiel. Ukážeme ti to na príklade postele, ktorú vlastní babička Červenej čiapočky. Nájdeš si na nej nejaké body a určíš ich polohu v súradnicovej sústave. Súradnice bodov oznámiš počítaču a oznámiš mu aj to, ktoré body majú byť spojené. On vďaka tomu vie, na akom mieste má nakresliť body a ako majú byť spojené.

V realite to funguje tak, že grafik vytvorí v programe (napr. Blender) objekt. Povrch objektu sa skladá z veľmi veľa bodov, ktoré sú pospájané do trojuholníčkov. Program vygeneruje textový súbor, kde sú napísané súradnice všetkých bodov a je tam aj napísané to, ktoré body majú byť spojené. Iný program (v ktorom sa robí hra) tento súbor prečíta a objekt zobrazí.

Super, okrem postele nám grafici vytvorili aj ostatné objekty patriace do Červenej čiapočky. Všetky sú reprezentované bodmi, teda máme akési množiny bodov, s ktorými vieme ďalej počítať. Prvú časť vývoja hry máme teda za sebou.

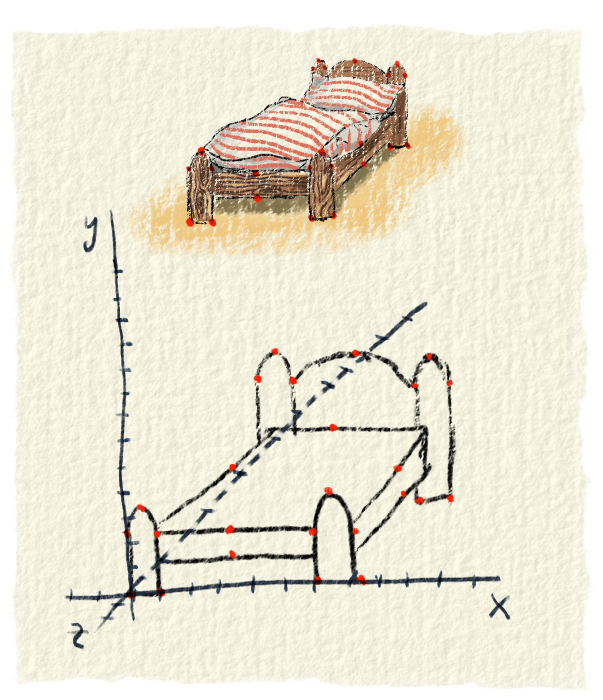
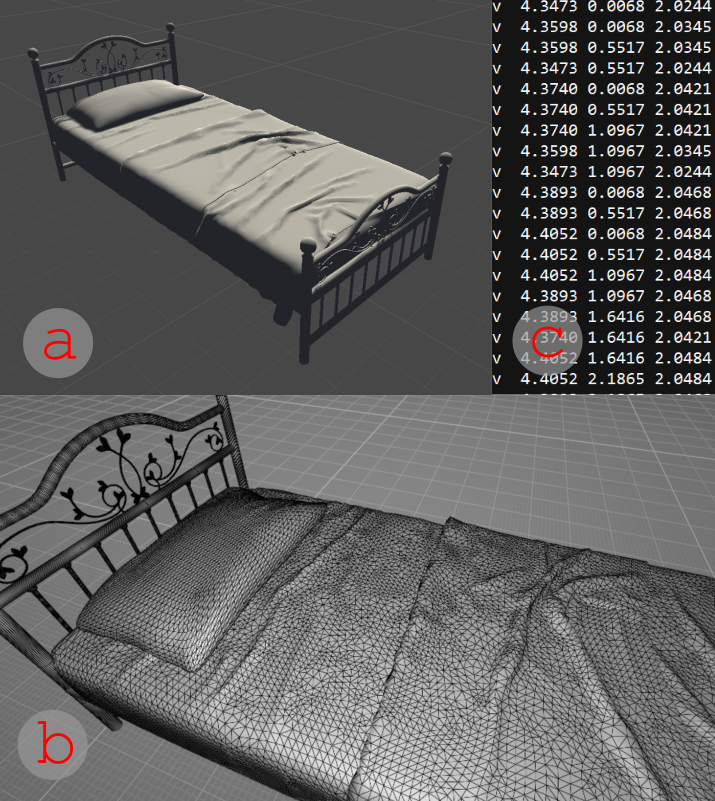
Vektory

Všetky objekty poslušne čakajú zapísané v súboroch. Chceme ich trochu rozhýbať. Najprv si ale musíme vysvetliť, ako taký pohyb v počítačoch funguje. Naučíme sa niečo o programoch na vývoj hier a o tom, ako funguje animácia.

Programy na vývoj hier

V hrách treba, aby sa objekty hýbali a prípadne aspoň trochu poslúchali fyziku nášho sveta. Nechceme predsa, aby Červená čiapočka vyletela do vesmíru, keď zakopne o kameň. Chceme, aby pekne poslúchla gravitáciu a capla na zem.

Vývojári hier zvyčajne nerobia celú fyziku od základu, ale používajú programy, v ktorých sa robia hry. Tie už fyziku obsahujú, takže vývojárom ju už stačí len použiť. Spomenieme len niekoľko prírodných zákonov, ktoré sa dodržiavajú v hrách. Je to už spomínaná gravitácia, trenie, hmotnosť objektov, pôsobenie síl, plynutie času, pohyb. Náš skutočný svet ovplyvňuje oveľa viac zákonov. Nie je možné ich všetky nasimulovať, lebo by na ne nestačil ani ten najvýkonnejší počítač na svete.

Animácia

Program nám už zabezpečil, že fyziku potrebnú na pohyb máme spočítanú, no pohyb treba aj nejako zobraziť. Pohyblivým obrázkom sa hovorí animácia.

Keď si bol menší, možno si skúšal v zošite na kraji strán nakresliť napríklad panáčika, ktorý skáče. Na každú stranu si nakreslil kúsok jeho pohybu. Na prvej strane stojí na zemi, na druhej je už vo vzduchu, na tretej je viac vo vzduchu, a tak ďalej, kým nebude znovu na zemi. Keď si strany rýchlo prehŕňal, zdalo sa ti, že sa panáčik hýbe. Deje sa to vďaka tomu, že náš mozog nedokáže vnímať rýchlo meniace sa obrázky, a tak si ich spája do jedného, ktorý sa pohybuje.

Na tomto fakte sú založené filmy aj hry. Kedysi sa animované filmy robili tak, že umelci ručne kreslili film, obrázok po obrázku. Na každom obrázku postavy o kúsok pohli. Obrázky sa potom nafotili a keď sa pustili rýchlo za sebou, zdalo sa, že sa veci vo filme hýbu. Toto bolo časovo veľmi náročné.

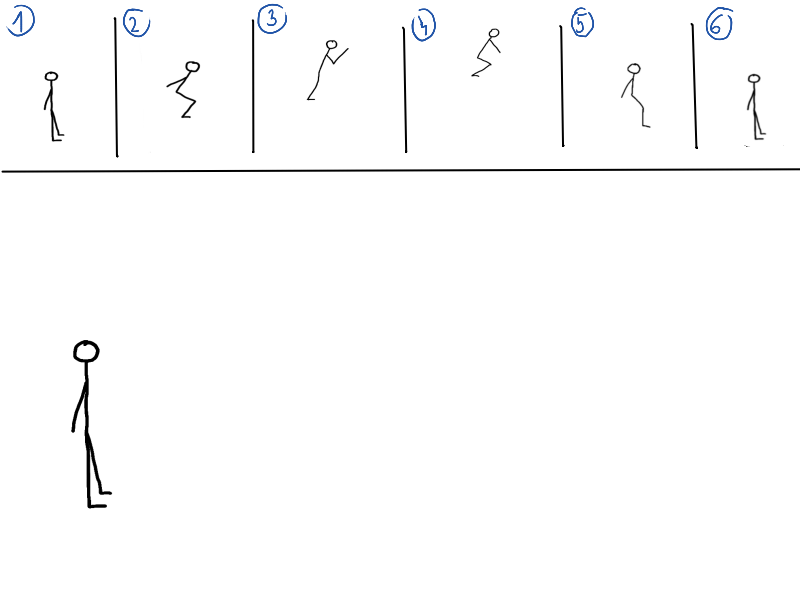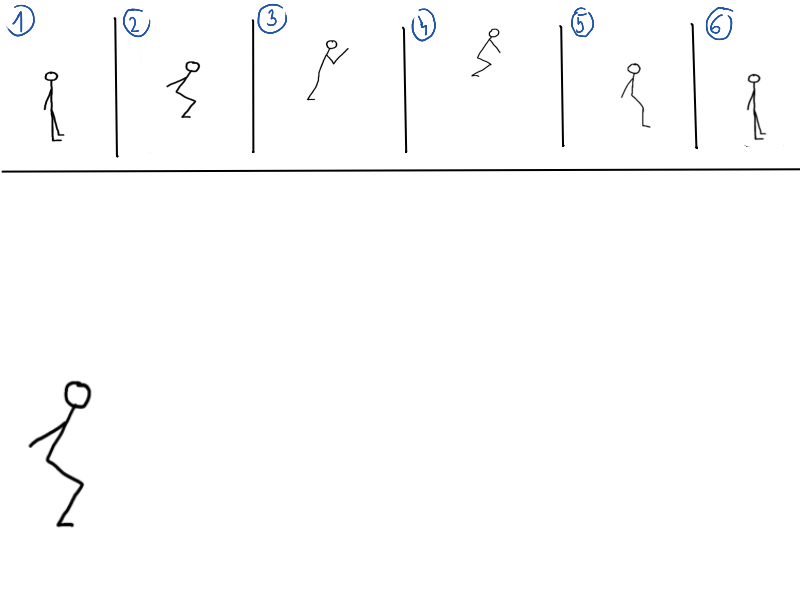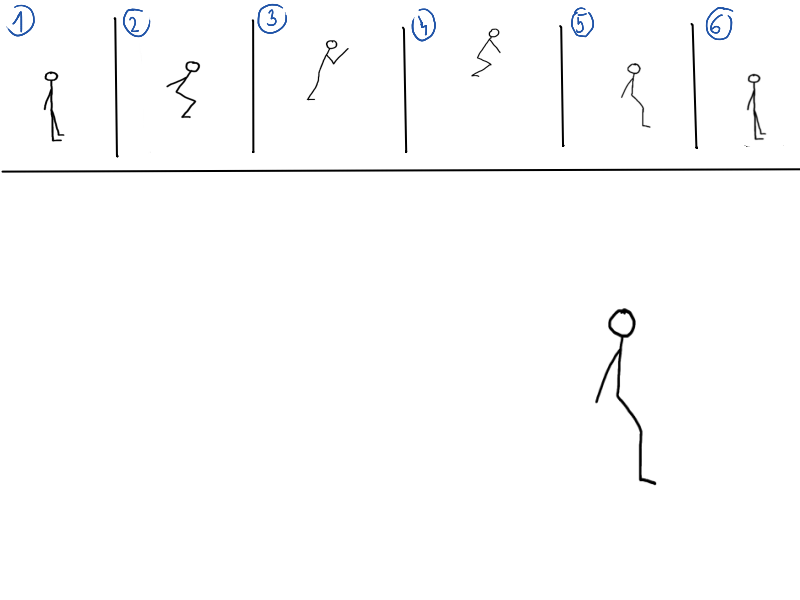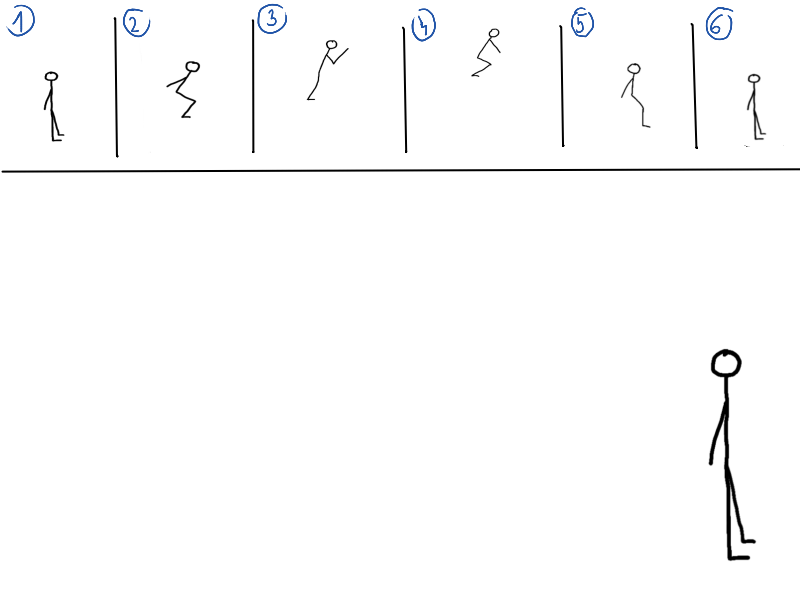
Jeden z prvých animovaných filmov bol Snehulienka a sedem trpaslíkov. Film robili tvorcovia od roku 1934 po 1937, teda tri roky. Na filme pracovalo vyše 750 umelcov, spravili viac ako 2 000 000 skíc a samotný film sa skladal z 250 000 obrázkov. Uznáš sám, že nakresliť toto všetko ručne bola riadna makačka. [1]

Dnes sa už obrázky nekreslia ručne, ale generujú ich počítače. Vďaka znalostiam fyziky a matematiky vedia, o koľko majú objekty posunúť v ďalšom obrázku.

Vektory použité v pohybe

Pohyb objektov v počítačových hrách sa snaží napodobňovať pohyb v našom svete. Pýtame sa, aký veľký kus cesty prejde objekt za nejaký čas. Zvykne sa to udávať v metroch za sekundu. Teda koľko metrov prejde objekt za jednu sekundu.

Podobne je to aj pri hrách. Program zvyčajne vykresľuje obrázky každých 0,02 sekundy. To znamená, že chceme vedieť, kam sa objekt pohol a potom ho na tom mieste vykresliť. To o koľko sa objekt pohne, nám hovorí vektor. Kde bude objekt zistíme tak, že vektor pripočítame k pozícií objektu. Objekt sa následne vykreslí.

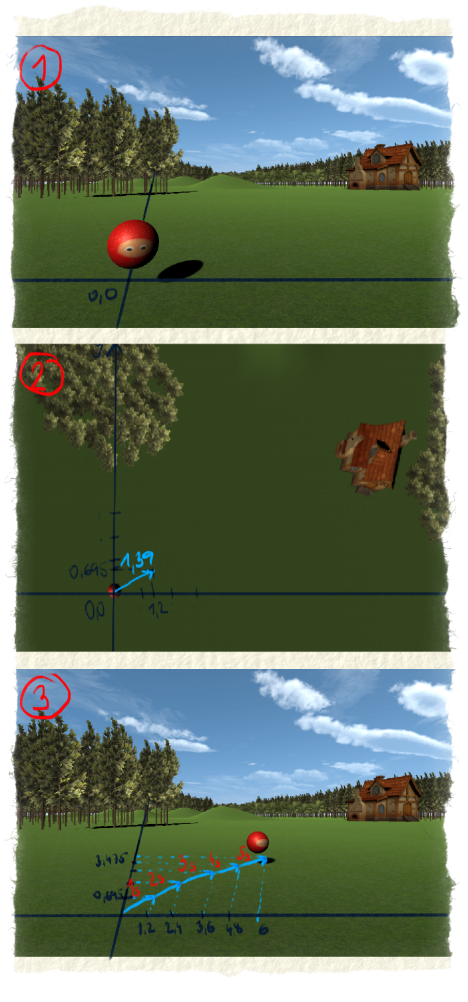
Ukážeme si to na Červenej čiapočke. V skutočnom svete človek chodí rýchlosťou 5km/h, čo je 1,39m/s. Karkulka sa teda pohne každú sekundu o 1,39 metra. Povedali sme si, že počítač vykresľuje obrázky každých 0,02 sekundy. Musíme teda zistiť, o koľko sa pohne Čiapočka za tento čas. Je to 1,39*0,02 = 0,0278. Čiapočka bude v nasledujúcom obrázku o 0,0278 metra ďalej.

V počítači sa to spraví tak, že sa spraví vektor rýchlosti. Zvyčajne sa udáva v m/s a potom sa prenásobí s časom (to je tých 0,02 sekundy). Veľkosť vektora je rýchlosť. Súradnice vektora udávajú jeho smer, lebo hovoria o tom, po ktorej osi sa má objekt pohnúť a o koľko. Pred vykreslením obrázku sa vektor pripočíta k súradniciam objektu. Objekt sa už vykreslí na nových súradniciach.

Na obrázku budeme počítať, o koľko sa pohne Karkulka za sekundu. Tých 0,0278 je príliš malých na kreslenie.

FPS

Možno si sa už niekedy stretol so skratkou fps, čo znamená frames per second, po slovensky počet obrázkov za sekundu. Túto skratku môžeš vidieť napríklad v súvislosti s hrami, filmami či videami. Znamená to, že koľko obrázkov sa vykreslí za jednu sekundu. Dnes sa normálne používa 24 fps. Niektoré hry majú 60 fps. Čím je fps vyššie, tým sú rýchlejšie scény (napr. pohyb vystreleného puku) kvalitnejšie, ale objem dát je väčší. Slabší počítač nemusí stíhať obrázky vykresliť.

Priesečník bodu a priamky

S objektmi sme už spravili skoro všetko, okrem jednej veci. Nezobrazili sme ich na obrazovku. Práve to ideme teraz urobiť, ale najprv musíme vedieť niečo o tom, ako taká obrazovka funguje.

Pixel

V dnešnej dobe sa väčšina obrazoviek skladá z pixelov. Pixel je taký mini-mini-mini štvorček, ktorý sa dokáže rozsvietiť na rôzne farby. Na obrazovke je ich veľmi veľa, napríklad 4K obrazovky majú po šírke 3 840 a po výške 2 160 pixelov. To je spolu 8 294 400 pixelov. Každý z nich sa dokáže rozsvietiť na inú farbu a tak zobraziť nejaký obrázok. Čím je pixelov viac, tým je obrázok kvalitnejší a je na ňom vidieť viacej detailov. Technické pozadie fungovania pixelov necháme na inokedy. Teraz nám stačí vedieť, že sú.

Raycasting a raytracing

Raytracing je jeden z najznámejších spôsobov zobrazovania objektov v hrách. Jeho jednoduchšia podoba sa nazýva raycasting a tú si vysvetlíme.

Všetky objekty v hre Červená čiapočka sú 3D, sú umiestnené v súradnicovej sústave, skladajú sa z veľmi veľa trojuholníčkov a každý trojuholníček má svoju farbu. Objekty potrebujeme nejako zobraziť na našej štvorčekovej obrazovke.

Túto úlohu berie na seba raycasting. Zoberie si ten náš svet z hry a akože doňho umiestni obrazovku. Z každého štvorčeka na obrazovke spraví priamku a vypočíta, či sa náhodou nestretla s nejakým trojuholníčkom objektu. Ak priamka preťala trojuholníček, tak sa zoberie jeho farba a vyfarbí sa ňou štvorček na obrazovke.

Priamka, ktorou zisťujeme, či z daného štvorčeka obrazovky niečo vidíme alebo nie, sa nazýva lúč. Tento lúč vychádza z miesta, z ktorého sa pozeráme cez obrazovku na scénu. Toto miesto sa nazýva kamera, ale v skutočnosti to naozajstná kamera nie je. Je to nejaký bod v súradnicovej sústave, ktorý sa nachádza za našou obrazovkou. Toto je bod, ktorý v lúči poznáme. Ďalej poznáme aj smer, ktorým ide lúč. Vieme si ho vypočítať z toho, cez ktorý štvorček sa práve pozerá. Poznáme teda bod a smer. To sú dve veci, z ktorých vieme zložiť priamku. Dostávame tak parametrickú rovnicu každého lúča. To je fajn, to potrebujeme.

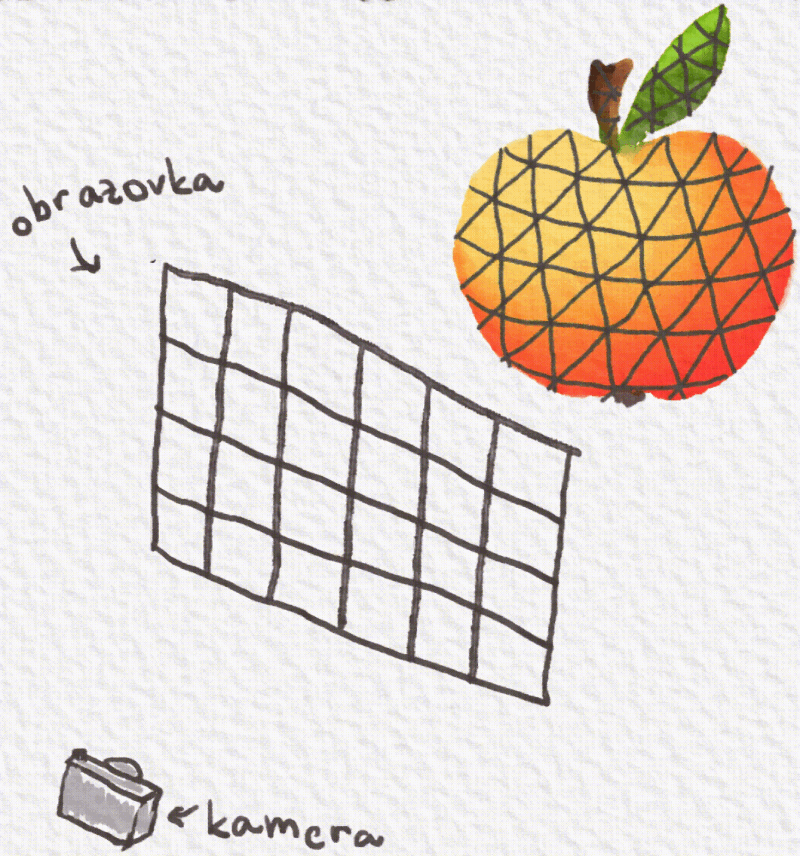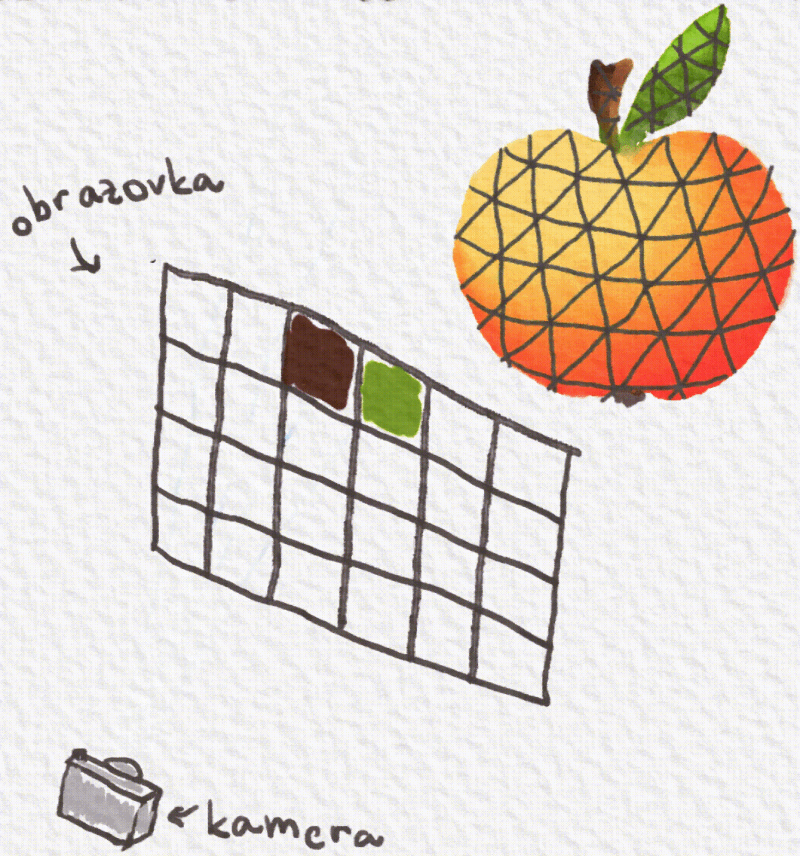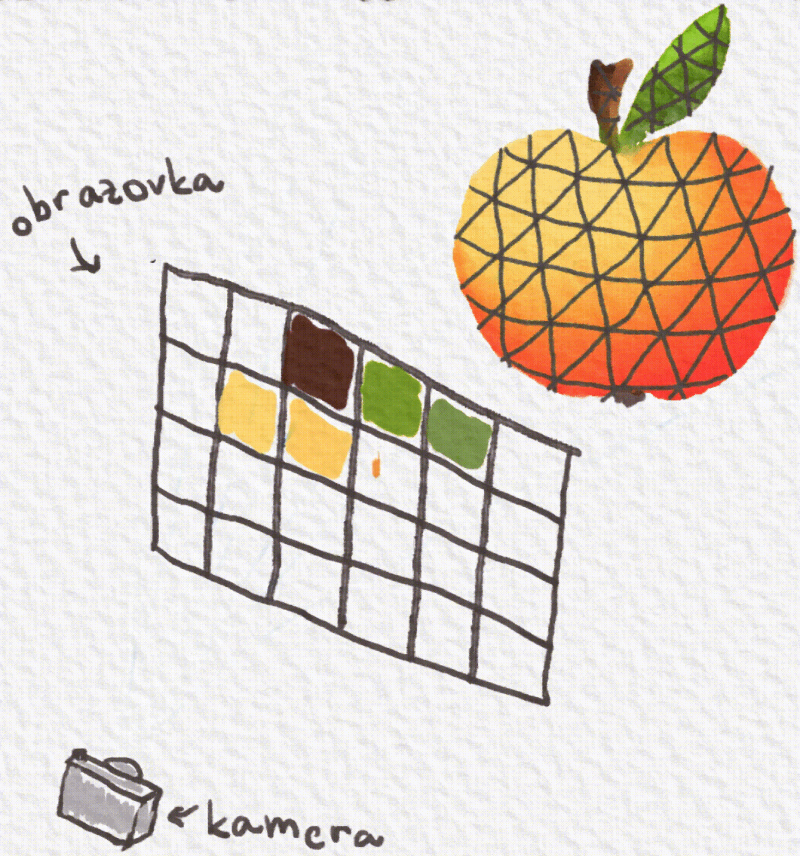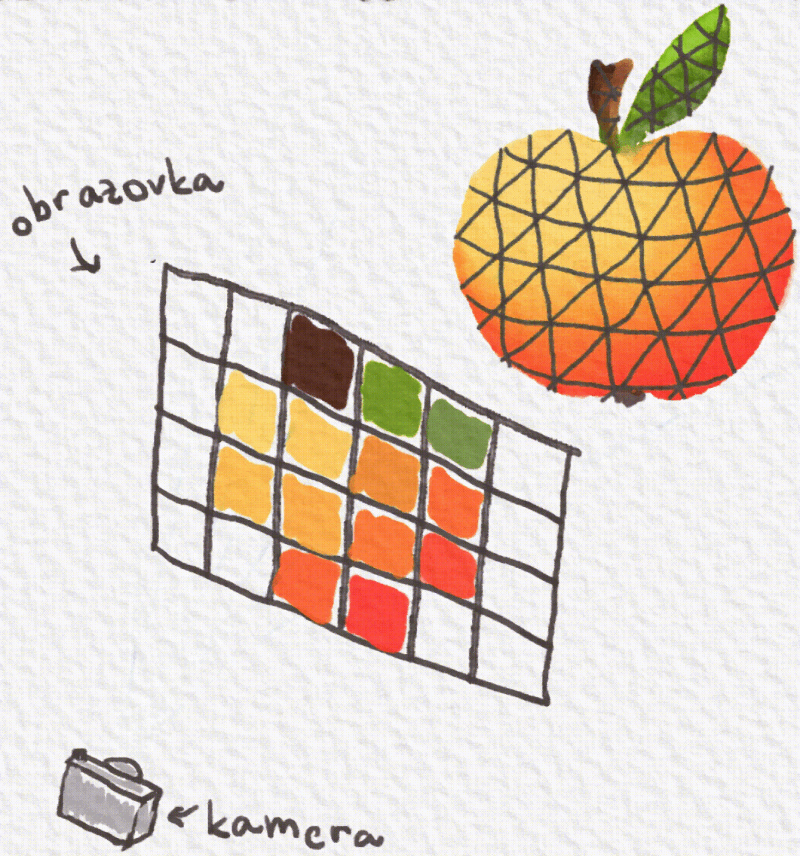
Ďalej vieme niečo o objektoch. Vieme, že sa skladajú z trojuholníčkov a súradnice ich bodov máme zapísané v súbore. V každom trojuholníku poznáme tri body. Pri rovinách sme si povedali, že rovina je tvorená tromi bodmi. Takže vieme zostrojiť rovnicu roviny pre každú tú malú plôšku, z ktorej sa objekt skladá.

Dokonca vieme zistiť aj to, či a kde sa rovina a priamka pretnú. Spravíme to jednoducho tak, že bod vyjadrený parametrickou rovnicou priamky dosadíme do rovnice roviny. Keď nám vyjde parameter t nejaké číslo, tak vieme, že priamka pretla rovinu. Samotné t nám dokonca hovorí o tom, že ako ďaleko je ich prienik.

Keď sa priamka s rovinou pretnú, ešte sa kontroluje, či priamka preťala rovinu "vnútri" toho trojuholníčka. Rovnica roviny totiž definuje celú rovinu, nie len ten trojuholník.

Raycasting z matematického hľadiska funguje tak, že si pre každý pixel obrazovky vytvoríme lúč. Tento lúč je priamka, ktorá začína niekde u pozorovateľa (normálne sa to povie, že v kamere) a prechádza cez daný pixel. Vieme ju vyjadriť parametrickou rovnicou. Pre každý lúč sa zoberú všetky objekty, prejdú sa trojuholníček po trojuholníčku a skontroluje sa, či náhodou priamka daný trojuholníček nepretla. To môžeme spraviť vďaka tomu, že z trojuholníčka vieme zistiť rovnicu roviny a potom môžeme vypočítať priesečník lúča s touto rovinou. Ešte sa skontroluje, či prienik leží vnútri trojuholníčka a nie niekde mimo neho. Ak vieme, že lúč preťal trojuholníček, zoberieme jeho farbu a namaľujeme ňou pixel. Takto vieme zobraziť na monitor aj tie najkomplexnejšie scény z hier a filmov.

Zatiaľ sme zabudli na jednu dôležitú vec. Na svetlo. Raycasting zoberie len tú farbu, ktorú grafik pre daný trojuholníček zapísal do súboru. Čo však, keď na trojuholník dopadá svetlo alebo je v tieni? Vtedy je farba trochu iná. Ako má vyzerať farba v tieni a ako na svetle vieme vypočítať, ale ako vieme, či je objekt na svetle alebo ho niečo zatieňuje?

Do súradnicovej sústavy našej scény umiestnime niekde bod, ktorý bude predstavovať svetlo (slnko/lampu/oheň/čokoľvek). Dôležitá poznámka: smer, ktorým svieti svetlo vieme. Keď lúč pretne trojuholník, tak sa hneď neberie z neho farba, ale skontroluje sa, či je na svetle alebo v tieni. Spraví sa to tak, že sa vyšle ďalší lúč, nazvime ho "shadow ray". Začína v bode, kde sa pretla priamka s plochou a smeruje do svetla. Ak "shadow ray" na svojej ceste za svetlom narazí na nejaký iný objekt, znamená to, že náš objekt je v tieni. Ak nezaznamená žiaden prienik, náš objekt je na svetle.

Naše objekty budú teraz pekne vyfarbené a dokonca tie, ktoré majú byť v tieni, budú v tieni. Žiaľ ešte stále sa ani zďaleka nepribližujeme k realite. Aby sme sa však ešte viac podobali nášmu svetu, treba počítať s ďalšími vecami. Je to odraz svetla na lesklých materiáloch (napr. zrkadlo) a prepúšťanie svetla cez priesvitné materiály (napr. sklo). Na ich výpočet sa vytvárajú ďalšie lúče a počítajú sa ďalšie prieniky. Pridanie lúčov, ktoré sa odrážajú alebo prechádzajú cez materiály, pre nás znamená, že sme sa dostali od raycastingu k raytracingu. To je však už trochu dlhšia rozprávka. Nastal čas, aby zazvonil zvonec a vývoju hry o Červenej čiapočke bol koniec 😊 .

Vďaka takejto matematike, možno jednoduchej a možno strašidelnej, vedia počítače takto pekne zobrazovať svetlo.

Koniec hry o Červenej čiapočke

Zazvonil zvonec a vývoju hry je koniec. Náš unikátny výtvor sme zavesili do obchodu s apkami a už len čakáme na to, kedy budeme milionármi. Ak chceš byť tiež milionár, tu sú nejaké ďalšie nápady na hry: Snehulienka, 12 mesiačikov, Šípková Ruženka. Tieto nápady na originálne hry čakajú len na teba, kedy sa naučíš matiku. Tak sa ju uč, nech nemusia čakať dlho 😉.

Zdroje