Kvadratická funkcia
Funkcie opisujú ako sa nejaká hodnota mení na základe inej. Napríklad ako sa mení prejdená dráha v závislosti na čase, stav bankového účtu na základe vkladania peňazí ale aj odhadovanie veľkosti populácie nejakého živočícha v závislosti na počasí (napr. priemernej teplote na jar).Keďže rôzne veci sa menia rôzne, treba vymyslieť aj rôzne opisy týchto zmien, teda funkcie. Kvadratická funkcia je jednou z nich. Opisuje takú zmenu, že sa mení nejaká veličina a ešte sa mení aj táto zmena.
Napríklad by sme do banky vkladali každý mesiac peniaze a sledovali by sme stav účtu. Nedávali by sme však stále rovnako peňazí, ale každý mesiac by sa vkladaná čiastka navýšila o rovnakú sumu. Napr. prvý mesiac by sa dalo euro, druhý by sa dali tri eurá, tretí mesiac by sa vložilo päť eur. Skrátka vždy by sa vkladaná suma navýšila o dve eurá. Stav účtu by sa potom dal opísať kvadratickou funkciou.
Samozrejme stav účtu nemusí iba rásť, môže aj klesať. Kvadraticky by klesal vtedy, keby každý mesiac z neho vyberieme o rovnakú sumu viac ako minule
Na to, aby sme lepšie pochopili, čo je kvadratická funkcia zač, treba sa pozrieť na jej vznik. Aspoň trochu 🙂
Ako vznikla kvadratická funkcia
Svoj názov dostala zhruba v roku 1660 podľa latinského slova quadratum [1], čo znamená štvorec. Jej pomenovanie je veľmi výstižné, pretože kvadratickú rovnicu (nie ešte kvadratickú funkciu) používali národy po tisícročia v súvislosti so štvorcami. Oni potrebovali rozdeľovať pôdu a stavať stavby. Pri tom sa im často stávalo, že poznali rozlohu pôdorysu alebo pozemku a potrebovali nejak zistiť jeho strany.[2]Prvé kvadratické problémy sú známe už zo starovekého Egypta, kedy jeho obyvatelia potrebovali zistiť dĺžku strán pozemkov a stavieb. Oni síce vedeli vypočítať obsah štvorca a obdĺžnika ak poznali jeho strany. No naopak to išlo ťažko. Vyvinuli si na to nejaké postupy. Tie však boli zdĺhavé a egyptské písmo bolo zložité, tak si strany pre rôzne obsahy predpočítavali do tabuliek. Keď poznali strany a chceli vedieť rozlohu, stačilo im pozrieť do tabuliek. Lenže toto nebolo veľmi dobré riešenie, pretože v tabuľke nemohli mať zapísané všetky rozlohy a ani všetky strany. Často teda počítali iba približne. A to nie je dobré, ak chcete vyberať dane.[2]
Ako nájsť strany, keď je známy obsah trápilo aj Sumerov. Vďaka jednoduchšiemu písmu našli trochu všeobecnejšie riešenie ako boli tabuľky. Vytvorili postup na nájdenie strán obdĺžnika. Problém bol zhruba takýto. Vieme, že jedna strana obdĺžnika je veľká x. Druhá strana je o b stôp dlhšia ako x. Ako veľké sú strany obdĺžnika? To b sa poznalo, takže stačilo už iba vyrátať x. Sumeri vymysleli na to niečo, čo dnes poznáme pod názvom metóda doplnenia na štvorec. O nej si povieme inokedy, pretože dnes riešime kvadratické rovnice vzorcom, ktorý je odvodený práve z tejto metódy.[2]
Postupom času sa objavovali ďalšie kvadratické problémy a s nimi aj ďalšie tvary dnešných rovníc. Vtedy to však boli iba geometrické riešenia a neskôr rovnice s číslami. Stále to však nebolo nič všeobecné a na každý problém muselo byť zvlášť riešenie. Napríklad vtedy bola pre nich iná rovnica $x^2+6=0$, iná $8x^2=0$ a iná $x^2+4x=0$. Samozrejme rovnice neboli napísané písmenkami, ale slovami a číslami.[2]
Preto ľudia stále hľadali všeobecnú rovnicu. Až ju nakoniec našiel indický matematik Brahmagupta[2]. Neskôr sa do matematiky pridali písmenká a tak dnes máme tvar kvadratickej rovnice takýto: $$ax^2+bx+c=y$$ Až neskorší rozvoj matematiky v sedemnástom a osemnástom storočí priniesol používanie kvadratickej rovnice ako funkcie.
Rozdiel medzi kvadratickou funkciou a kvadratickou rovnicou
Aký je rozdiel medzi funkciou a rovnicou?Funkcia je taká vec, do ktorej sa dosadia čísla za x a ona vráti výsledok y.
V rovnici práve naopak, je známy "výsledok" y a cieľom riešenia rovnice je nájsť x, ktoré viedlo k výsledku.
Zhrnutie: v rovnici je známe y a ráta sa x. Vo funkcii je známe x (lebo sa zaň dosádzajú čísla) a hľadá sa y.
Kvadratická funkcia
Ľudstvo o kvadratických problémoch vedelo už dávno. Keďže tých problémov bolo veľa, chceli to zapísať nejak všeobecne. Pretože keby sa vie vyriešiť všeobecná funkcia, tak by sa vedel vyriešiť aj každý z tých problémov. A tak sa ľudstvo postupom času dopracovalo k zápisu kvadratickej funkcie, aký poznáme dnes: $$f(y)=ax^2+bx+c$$ Môžeme si ukázať jednotlivé zložky kvadratickej funkcie. Že čo vlastne znamenajú.f(y) - to je výsledok. Keď si za x dosadíme nejaké číslo a vyrátame preň tú funkciu, tak f(y) je výsledok. Napríklad mali by sme funkciu $f(y) = 1,5x^2 - 4x + 3$. Za x by sme dosadili napríklad 8,3, tak by sme dostali:
$$ f(8,3) = 1,5\cdot8,3^2 - 4\cdot8,3 + 23 = 103,335 - 33,2 + 23 = 93,135 $$
Teda výsledok funkcie v bode 8,3 je 93,135.a,b,c - sú koeficienty. Ich hodnoty sú známe. Teda v takom bežnom zápise funkcie to nebudú písmenká, ale už nejaké konkrétne čísla. O tom, prečo sú dôležité si povieme neskôr.
x - to je premenná. Za ňu sa dosádza číslo, pre ktoré treba vedieť výsledok funkcie. Keď sa funkcia kreslí do grafu, tak sa tieto čísla zakresľujú na osi x.
x2 - dosadí sa tam to isté číslo, čo za x, ibaže sa umocní na druhú. Toto x2 opisuje práve tú zmenu zmeny.

🦉 ÚLOHA
Skús si spraviť podobnú tabuľku pre viaceré $x^2$. Pre každé vyrátaj zopár základných hodnôt, vyrátaj rozdiely medzi nimi a ešte vyrátaj aj rozdiely medzi týmito rozdielmi. Tu je zopár inšpirácii:- $2x^2$ pre hodnoty 1.1, 1.2, 1.3, 1.4, 1.5
- $1,5x^2$ pre hodnoty -4, -3, -2, -1, 0, 1, 2, 3, 4
- $-x^2$ pre hodnoty 0, 1, 2, 3, 4, 5
Koeficienty kvadratickej funkcie
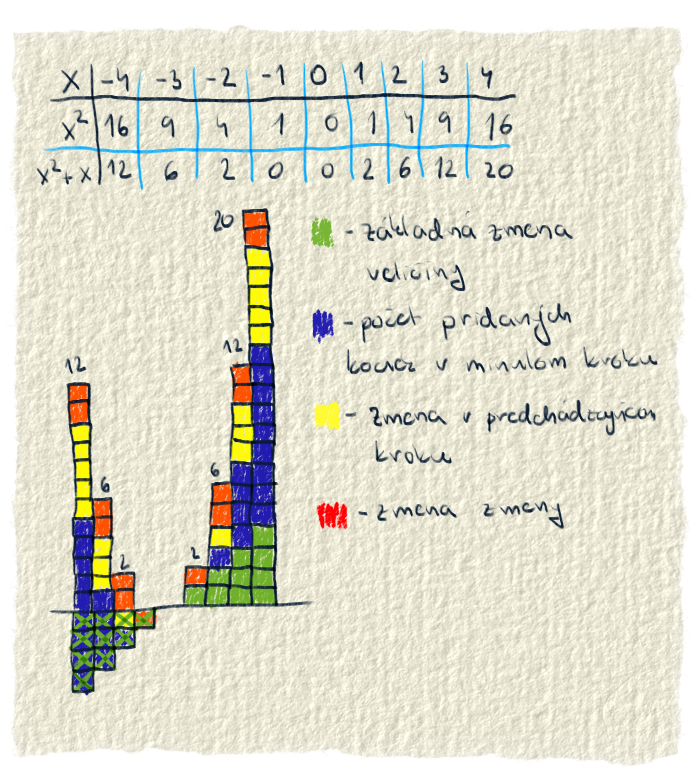
Zákonitosť, s akou sa mení kvadratická funkcia sa dá celkom pekne vysvetliť na kockách.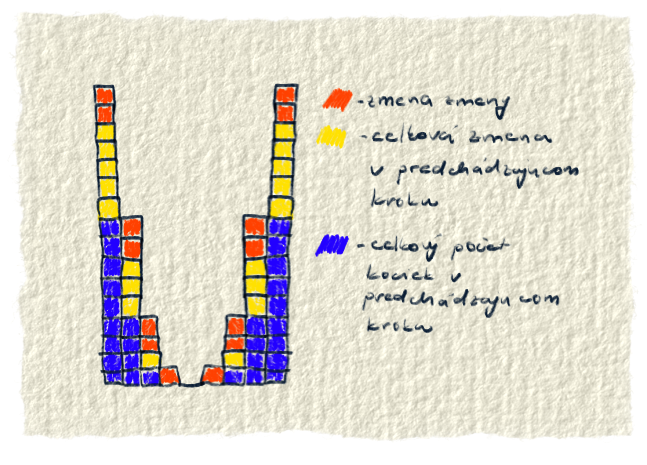
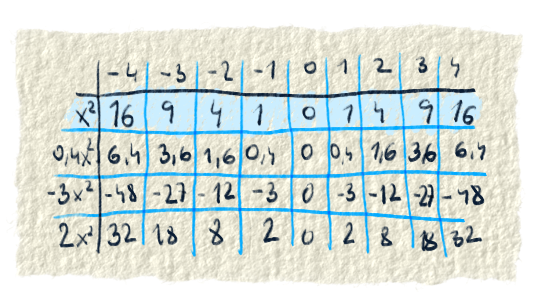
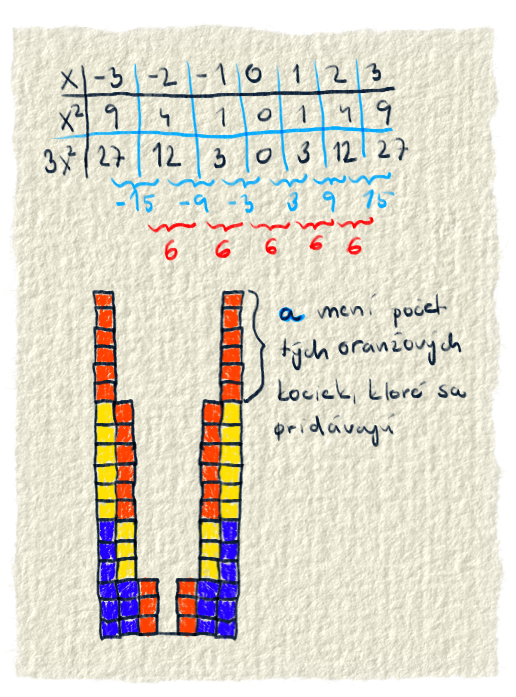
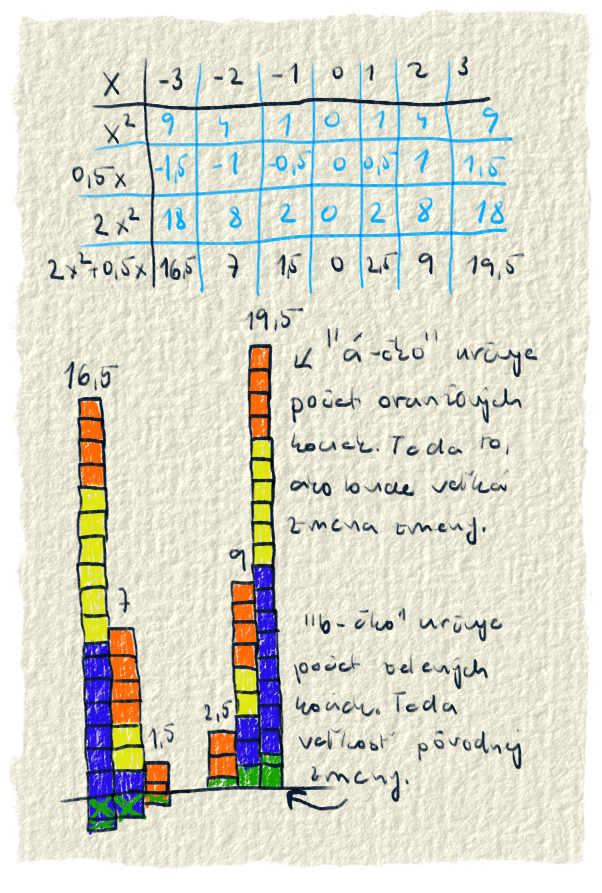
Teraz je na rade koeficient a. To je číslo, s ktorým sa násobí $x^2$. Spôsobuje to, že veľkosť $x^2$ môže byť ľubovoľne veľká. Lebo tým, že sa nejaké číslo násobí iným, tak ho vieme meniť, zväčšiť, zmenšiť či dať do záporu.
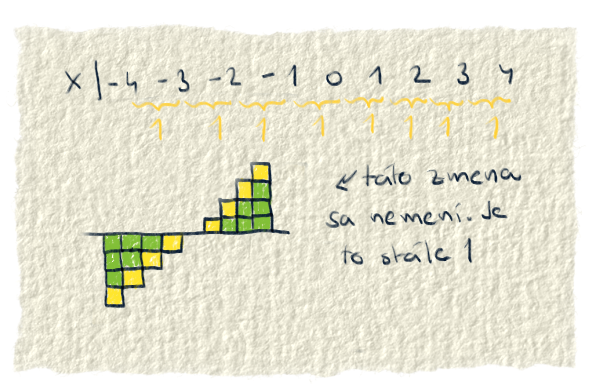
🦉 ÚLOHA
Skús nakresliť kocky pre nasledujúce funkcie:- $f(x)=4,5x^2$
- $f(x)=4,5x^2+2x$
- $f(x)=4,5x^2+2x+1$
Graf kvadratickej funkcie
Aby sa ľuďom lepšie rozmýšľalo nad vecami, ktoré reprezentuje kvadratická funkcia, je celkom užitočné si ich nejako zobraziť. Dá sa to všelijako, napríklad aj kockami, ako sme to robili doteraz. Ibaže to je nepresné (ťažko z toho vyčítame aspoň približnú hodnotu napr. pre x=1,5) a z vlastnej skúsenosti už vieš, že aj namáhavé. Inteligentnejší spôsob sú napríklad tabuľky a grafy. V tabuľke vidíme presné hodnoty a v grafe zase tú funkciu tak celkovo.Graf funkcie sa robí jednoducho. Zoberú sa nejaké x, vyrátajú sa pre ne hodnoty y. Na papier sa nakreslia dve kolmé čiary. Na tú rovnú sa spravia guličky tam, kde majú byť x a na tú zvislú sa nakreslia guličky tam, kde má byť y. To sa potom pospája.
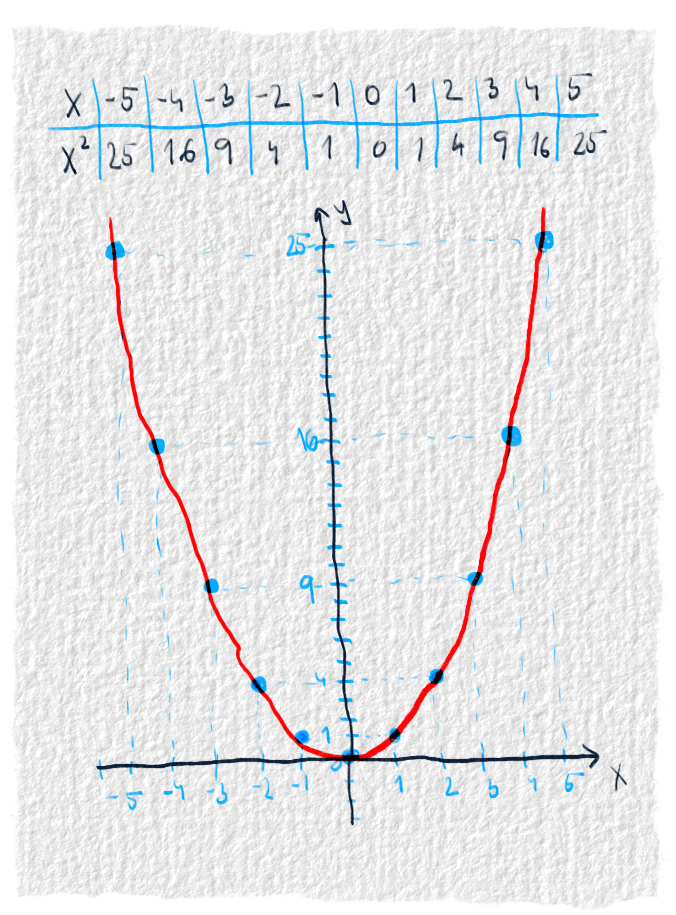
$x^2$ spraví z grafu parabolu - niečo podobné ako písmeno U. Všetky čísla, ktoré sa dosadia za x budú kladné. Pretože je to na druhú, číslo sa násobí samým sebou a + krát + aj - krát - je +. Tie výsledky nebudú však rásť stále rovnako, pretože výsledky pre susedné čísla sa budú stále viac a viac od seba líšiť, ako sa pôjde smerom od nuly.
Koeficient a ovplyvňuje veľkosť $x^2$, teda to, ako veľký bude rozdiel medzi susednými hodnotami. Čím väčšie bude áčko, tým budú výsledky rozdielnejšie. Čím je áčko menšie, tým budú aj rozdiely medzi susedmi menšie. Na grafe sa to prejaví tak, že bude to účko strmšie alebo čapatejšie. Negatívne áčko všetky tie hodnoty dá do mínusu a graf bude hore nohami. Už to nebude účko, ale kopec.
Pridanie členu bx do funkcie spraví s grafom, takú zvláštnu vec, že keď sa mení veľkosť b, graf sa hýbe po parabole. Môžeš to vyskúšať na nasledujúcom grafe.
Stručné vysvetlenie je takéto:
$x^2$ je vlastne graf, kedy je b, teda tá počiatočná zmena nulová.
Pridanie bx do funkcie znamená, že na začiatku už bola nejaká zmena. Tým, že sa do funkcie pridal bx, čo je lineárny člen, deje sa tam to, že sa ku kvadratickej funkcii pričíta lineárna funkcia.
Teda ku každej hodnote sa priráta/odráta hodnota lineárnej funkcie bx v danom bode. Keď si vyrátame pár hodnôt do tabuľky, dá sa všimnúť, že v istom momente bude x väčšie ako $x^2$.
Vtedy to x preváži a hodnoty stiahne pod nulu, čiže kúsok toho grafu sa bude nachádzať pod osou x. Ten úsek je medzi priesečníkmi grafu s osou x.
Keď sa bude meniť iba b, ten graf bude robiť pohyb po parabole, lebo čím väčšie béčko, tým ešte väčšia y súradnica minima. Je to nadlhšie vysvetľovať, ak chceš príď na to sám, prečo sa to hýbe po parabole. Pomôcka môže byť, že si treba vyrátať y súradnicu minima/maxima funkcie a pozrieť sa na to, ako sa mení a ako sa ráta.
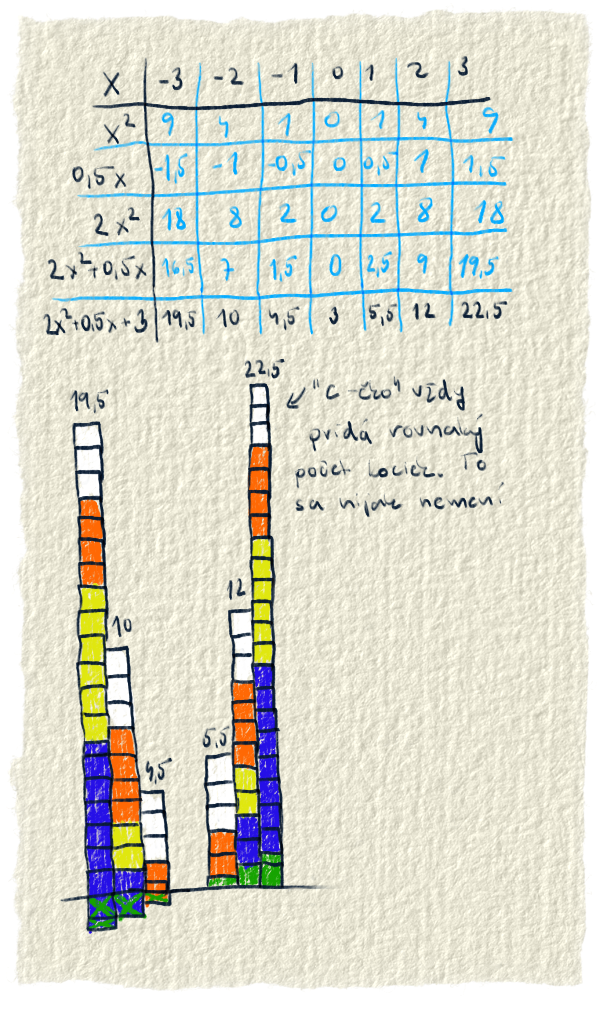
Koeficient c je číslo, ktoré sa pripočíta k výsledkom. Ku každému sa pripočíta rovnaké číslo, čiže všetky budú rovnako väčšie alebo rovnako menšie. To posúva graf hore dole po y osi.
🦉 ÚLOHA
Bez toho, aby si niečo počítal, nakresli grafy pre tieto funkcie. Mimochodom, na tých tvojich obrázkoch majú byť iba osi a parabola. Ide o to, či zhruba trafíš, ako má byť parabola vysoko, ako má byť otočená, či má byť strmá alebo čapatá a podobe.- $f(x) = x^2$
- $f(x) = 10x^2$
- $f(x) = 100x^2$
- $f(x) = -10x^2$
- $f(x) = x^2 + 20$
- $f(x) = x^2 - 5$
- $f(x) = x^2 + 3x$
- $f(x) = x^2 - 3x$
- $f(x) = 5x^2 + 5x + 5$
- $f(x) = -10x^2 - 10x - 10$
Kvadratická funkcia na príklade - rovnomerne zrýchlený priamočiary pohyb
Žijeme vo svete, kde veci menia svoju rýchlosť. Keby to tak nebolo, autobus by nikdy nemohol zastaviť na zastávke, pretože by nemohol spomaliť. Hokejista by nikdy nemohol dať gól, pretože ak by trafil puk, nemohol by ho zrýchliť na poriadnu strelu. Ani ty by si si nikdy nemohol sadnúť k raňajkám a musel by si ísť večne rovno dopredu.Aj napriek tomu, že veci menia svoju rýchlosť, chceme vedieť vyrátať vzdialenosť akú prešli za určitý čas. Takým jednoduchým príkladom môže byť aj auto, ktoré zrýchľuje alebo spomaľuje.
Zrýchlenie je zmena rýchlosti za čas. Nemusí to byť iba zrýchlenie akože zrýchlenie, ale je to aj spomaľovanie, že niečo brzdí. Tu sa budeme baviť o rovnomerne zrýchlenom priamočiarom pohybe. To znamená, že zrýchľovať sa bude konštantne (každú časovú jednotku sa zmení rýchlosť rovnako).
Poďme sa pozrieť na to, ako zrýchlenie funguje. Rýchlosť hovorí o tom, koľko nejakej dĺžky prejdeme za jednu časovú jednotku. Napríklad, koľko kilometrov prejdeme za jednu hodinu. Počas tejto hodiny sa môže meniť aj samotná rýchlosť. Vtedy hovoríme o zrýchlení.
Na začiatok budeme mať úplne najjednoduchší pohyb. Za jednu hodinu prejde auto jeden kilometer. Hádaj koľko kilometrov prejde auto za 5 hodín? Áno, je to 5, uhádol si, si šikovný.
Matematickým jazykom zapísané: $$s = 1t$$ UPOZORNENIE: nasledujú obrázky s modrým autom. Keď budeš na ne klikať/ťukať, auto sa bude hýbať.
Matematickou rečou zapísané: $$s = vt$$
Napríklad na začiatku hodiny auto stojí, počas nej zrýchli o $2km/h$, takže na konci hodiny pôjde auto rýchlosťou $2km/h$.
Na vypočítanie dráhy treba čas a rýchlosť. Čas, to si dosadíme a rýchlosť vypočítame pomocou zrýchlenia. Keď zrýchľujeme napr. $2km/h^2$, tak prvú hodinu máme rýchlosť $2km/h$, druhú už $4km/h$ a tretiu $6km/h$. Vo všeobecnosti sa to zapíše ako $v = at$.
Vypočítať dráhu pri zrýchlení nie je také ľahké, ako sme to robili doteraz. Vieme, že dráha sa počíta $s = vt$, ale čo je v tomto prípade v? Je lákavé tam dosadiť $at$. Treba si uvedomiť, že rýchlosť sa menila postupne a kvôli zrýchleniu nebola rovnaká počas celého času t. Potrebujeme vypočítať priemernú rýchlosť, ktorou sa objekt počas toho času pohyboval.
Ak sa vrátime k autu, ktoré má zrýchlenie $2km/h^2$, aká bude jeho priemerná rýchlosť počas prvej hodiny? No $2km/h$ to asi nebude, lebo na začiatku auto stálo. Keďže auto zrýchľovalo konštantne (stále rovnako), bude to logicky priemerná rýchlosť vyrátaná z rýchlosti na začiatku a na konci. Na začiatku je rýchlosť 0 a na konci 2. Priemer z tohto je $\frac{0+2}{2}$. Tá nula tam byť nemusí, čiže je to iba $\frac{2}{2} = 1$. Všeobecný zápis vyzerá takto (v našom prípade sa $t = 1$): $$\frac{at}{2}$$ A aká je prejdená dráha? Stačí už iba dosadiť priemernú rýchlosť $\frac{at}{2}$ do vzorca $s = vt$. Dostávame teda $s = \frac{at}{2}t$, po upravení na chochmesný tvar: $$s = \frac{1}{2}at^2$$ V prípade nášho auta, ktoré sa pohybovalo jednu hodinu a počas tejto hodiny malo konštantné zrýchlenie $2km/h^2$, a teda priemernú rýchlosť $1km/h$ je to 1 km.
Pri zrýchlení sa prejdená dráha mení za ten čas akoby dva razy zároveň. Lebo ju mení rýchlosť a zrýchlenie mení tú rýchlosť, ktorá mení dráhu.
Na začiatku tretej hodiny bude mať auto rýchlosť 4 $km/h$, počas nej zrýchli o 2 $km/h$, teda na jej konci bude mať rýchlosť 6 $km/h$. Dráhu, ktorú auto prešlo počas tretej hodiny znovu vyrátame ako priemer rychlostí, teda $\frac{4+6}{2} = 5 km$. Za tri hodiny auto spolu prešlo $1+3+5 = 9$ hodín. Skús si porozmýšľať nad tým, koľko kilometrov prejde auto po štvrtej a potom aj po piatej hodine.
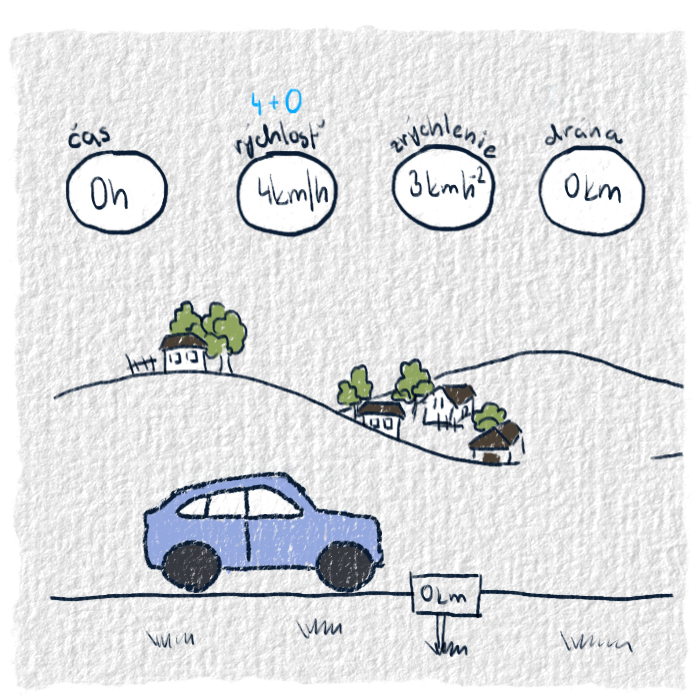
Napríklad na začiatku prvej hodiny má auto rýchlosť 4 $km/h$. Vďaka nej prejde tú hodinu 4 km. Keďže má ešte aj zrýchlenie 3 $km/h^2$, tak vďaka nemu prejde o 1,5 km viac, pretože na začiatku mal vďaka zrýchleniu rýchlosť väčšiu o 0 $km/h$ a na konci išiel o 3 $km/h$ viac, čo je $\frac{0+3}{2} = 1,5$. Spolu za tú prvú hodinu prejde $1,5km + 4km = 5,5km$.
Na začiatku druhej hodiny už ide 7 $km/h$ a stále zrýchľuje o 3 $km/h$, až na jej konci bude mať rýchlosť 10 $km/h$. Za druhú hodinu prejde $\frac{7+10}{2} = 8,5$. Za prvé dve hodiny auto prešlo $8,5km + 5,5km = 14km$.
A takto to bude pokračovať ďalej. Každú hodinu prejde auto o 4km viac, akoby prešlo, keby na začiatku stálo a nemalo žiadnu počiatočnú rýchlosť.
Zdroje
[1] HARPER, D. 2024. Online Etymology Dictionary. https://www.etymonline.com/search?q=quadratic
[2] Pflugerville. 2017. The History Behind The Quadratic Formula. https://www.mathnasium.com/blog/the-history-behind-the-quadratic-formula
[2] Pflugerville. 2017. The History Behind The Quadratic Formula. https://www.mathnasium.com/blog/the-history-behind-the-quadratic-formula
