Využitie analytickej geometrie

Analytická geometria sa používa preto, lebo geometrické problémy prevádza na algebraické. To znamená, že niečo, čo vieš nakresliť, prevedie na niečo, s čím vieš počítať. Analytická geometria vznikla na konci renesancie. Jej úlohou bolo dať odpovede astronómií, námorníctvu, obchodu a podobným veciam, ktoré si renesančný človek vymyslel. My sa prenesieme o pár storočí dopredu, do nášho letopočtu. Dnes sa bežný človek nesnaží objaviť novú galaxiu a ani si nerobí námornícky kurz. Zdalo by sa, že s analytickou geometriou sa stretne iba v učebniciach. Ale nie je to pravda. V rôznych veciach je skrytá na každom našom kroku.

Použitie v matematike

Súhlasím, nadpis použitie matematiky v matematike neznie užitočne, ale príklad je to pekný. Určite poznáš vzorec $(a+b)^2=a^2 + 2ab + b^2$. Vieme si ho takto nakresliť.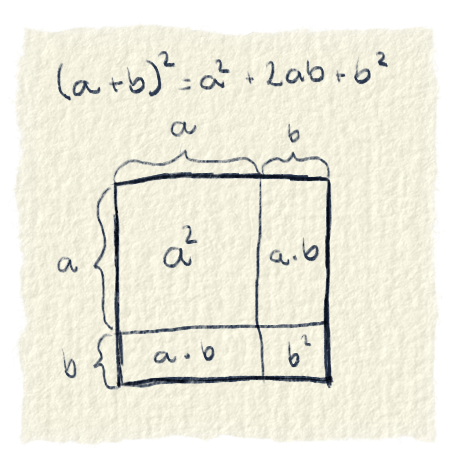

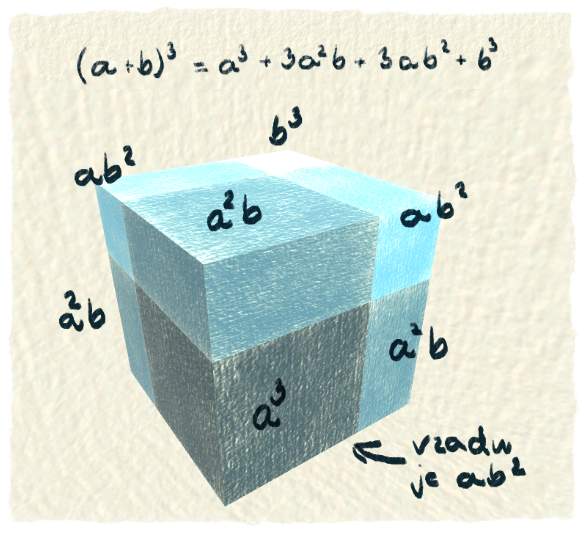
Podobne vieme geometricky vyjadriť aj vzorec $(a+b)^3$, iba namiesto štvorcov použijeme kocky.

Ak by sme mali používať iba geometriu, vzorec $(a+b)^4$ by neexistoval, pretože štvorrozmerné kocky nakresliť nevieme. Toto je príklad jednej peknej vlastnosti matematiky. Matematika totižto dokáže ísť za hranice sveta, ktorý poznáme a je tam až prekvapivo presná.

Zdroje