Priamka

V starovekom Grécku žil jeden pán. Volal sa Euklides. Rád sa bavil s geometriou a jednu jeho geometrickú myšlienku si požičiame. Euklides zistil, že keď zoberieme nejaké dva body, môže ísť nimi práve len jedna priamka (schválne si nakresli na papier dve bodky a sprav cez ne viac ako jednu čiaru...vidíš, nedá sa).

Teda stačia nám iba dva body na to, aby sme vedeli identifikovať priamku v priestore (to znamená, že keď mám nejakú svoju obľúbenú priamku, dokážem ju rozlíšiť od ostatných). V analytickej geometrii platí to isté. Priamku vieme zapísať dvomi bodmi.

Smerový vektor priamky

Niekedy nám to však nestačí (napríklad, keď chceme osvetliť objekty v počítačových hrách) a treba priamku vyjadriť pomocou bodu a smerového vektora. Smerový vektor priamky, je taký vektor, ktorý ukazuje smerom, ktorým ide priamka. Smerovým vektorom máme určený smer priamky a bodom jej polohu. Pozri sa na obrázok, čo by sa stalo, ak by sme poznali buď bod alebo smerový vektor a nie oboje.

Teraz ti dáme 5 minút času na to, aby si porozmýšľal, ako môžeme dostať smerový vektor. Nachystaj si stopky. Pripraviť sa. Pozor. Štart. Môžeš začať rozmýšľať……….Ok, 5 minút prešlo, a preto ti môžeme prezradiť riešenie 😀. Smerový vektor (tak ako každý vektor) vieme získať tak, že odčítame jeden bod od druhého. Hore sme napísali, že priamka je daná dvomi bodmi. Dva body ležiace na priamke máme a teraz stačí už len odčítať jeden od druhého.

Napríklad máme priamku danú bodmi A[1,2,3] a B[6,5,4]. Smerový vektor dostaneme ako $\vec{s}$ = B-A = [6-1; 5-2; 4-3] = [5; 3; 1]. Body sme odčítali po súradniciach. Teda x-ovú súradnicu A sme odčítali od x-ovej súradnice B. Pre y a z súradnice to platí rovnako.

Na opísanie priamky teraz môžeme použiť bod a smerový vektor. Okrem smerového vektora priamka má aj normálový vektor. Normálový vektor je kolmý na priamku. Vieme ho dostať zo smerového vektora tak, že mu otočíme súradnice a jednej z nich zmeníme znamienko. Smerový vektor $\vec{s}$ má súradnice [x,y], normálový vektor $\vec{n}$ bude mať súradnice [-y,x].

Parametrická rovnica priamky

Povedali sme si, že priamku vieme vyjadriť dvomi bodmi alebo bodom a vektorom. Ale čo tie ďalšie body ležiace na priamke. Veď priamka je zložená z nekonečne veľa bodov, ktoré na nej ležia. Tie už nevieme opísať?

Odpoveď je, že vieme. Všetky body, ktoré ležia na priamke vieme nejako opísať a aj to potrebujeme (tiež napríklad na to, aby v počítačových hrách fungovalo svetlo).

Teraz sa nám zíde nejaký bod na priamke a jej smerový vektor. Pri vektoroch sme si povedali, že keď k nejakému bodu pripočítame vektor dostaneme iný bod (ktorý je posunutý o ten vektor). Hovorili sme si aj, že vektorom vieme ľubovoľne meniť veľkosť tým, že ich násobíme číslom. Nachystaj si stopky, máš ďalších 5 minút a skús porozmýšľať, ako toto môžeme zužitkovať….

….Dobre, čas už uplynul a možno si prišiel na to, že by sme mohli k bodu prirátať vektor. Stále máme len dva body, ale keď ten vektor prenásobíme ľubovoľným číslom, dočiahneme na každý bod na priamke. Toto vieme po matematicky zapísať oveľa strašidelnejšie: $$ X=A+t\vec{s} $$ X je nový bod, ktorý chceme dostať. Bod A je ten, ktorý poznáme. Vektor $\vec{s}$ poznáme tiež, je to smerový vektor priamky. Písmeno t sa nazýva parameter. Zaň si dosádzame ľubovoľné číslo, podľa toho, na ktorý bod chceme dočiahnuť.

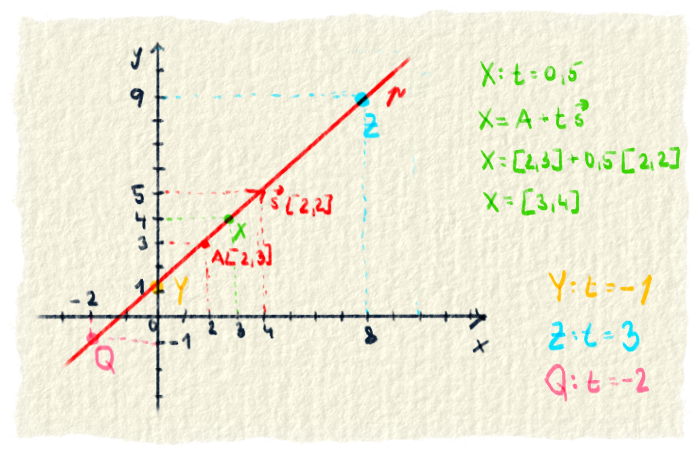
Všeobecná rovnica priamky

Každý bod na priamke vieme opísať aj všeobecnou rovnicou priamky. Napriek tomu ju používame trochu inak. Vďaka tejto rovnici vieme zistiť, či nami zvolený bod (označme ho X) leží na priamke.

Vyššie sme si povedali, že priamku vieme vyjadriť smerovým vektorom (označme ho $\vec{s}$) a bodom (označme ho A). Tieto dve veci využívame aj keď chceme zistiť či bod leží alebo neleží na priamke.

Zo smerového vektora $\vec{s}$ si spravíme normálový vektor $\vec{n}$. Normálový vektor je kolmý na priamku a teda aj na hocijaký iný vektor, ktorý je s priamkou rovnobežný. Teraz si spravíme vektor z bodu A do bodu X (vektor si označme $\vec{v}$). Ak je normálový vektor stále kolmý na náš vektor $\vec{v}$, tak bod leží na priamke. Ak nie sú kolmé, bod na priamke neleží.

Aby sme sa z obrázku dostali opäť do sveta analytickej geometrie, overíme si kolmosť vektorov pomocou skalárneho súčinu.

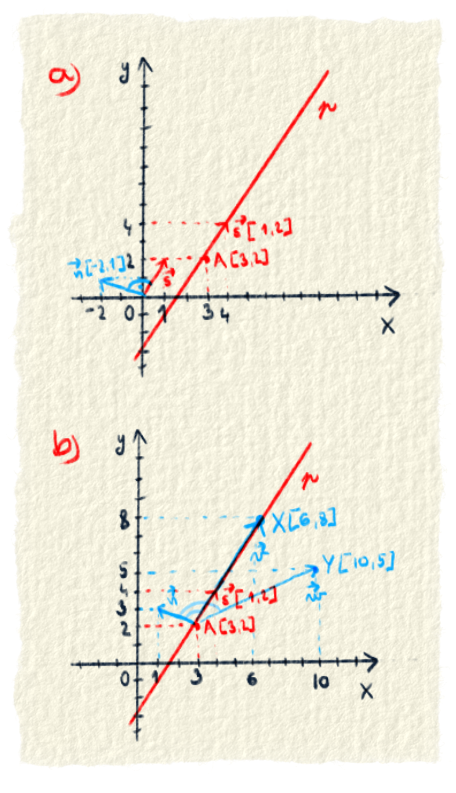
Prvý vektor, ktorý potrebujeme, je normálový vektor. Ten zo smerového vektora dostaneme otočením súradníc a pridaním mínuska k jednej z nich (nezáleží na tom ku ktorej, pretože vektor má vždy 2 normálové vektory, ktoré ukazujú len opačným smerom) $\vec{s}[s_x,s_y]\implies\vec{n}[-s_y,s_x]$.

Druhý vektor dostaneme z bodu A a z bodu X klasicky odčítaním súradníc $\vec{v}[x-a_x,y-a_y]$.

Teraz už len overíme, či sa ich skalárny súčin rovná 0. Ak rovnica bude platiť, bod leží na priamke. Rovnaký výsledok dostaneme, keď všeobecnú rovnicu odvodíme od parametrickej rovnice. Na chvíľu prehoďme kúsok rovnice na druhú stranu. $$ s_y x - s_x y = (s_y a_x - s_x a_y) $$ Z úprav, ktoré sme robili, vznikla rovnica, ktorá tiež hovorí o tom, či bod leží na priamke. Možno si si všimol, že tu porovnávame dva skalárne súčiny. Ak sú rovnaké, bod leží na priamke. Na ľavej strane rovnice je skalárny súčin normálového vektora $[s_y,-s_x]$ a vektora, ktorý má koncový bod v bode X. Na pravej strane rovnice je skalárny súčin toho istého normálového vektora a vektora, ktorý má koncový bod v bode A.

Teraz iba trochu upraceme písmená a dostaneme všeobecnú rovnicu priamky ako z učebnice. $$ \begin{align} s_y x - s_x y - (s_y a_x - s_x a_y) & = 0 \\ a x + b y + c & = 0 \end{align} $$ Malá úloha na záver. Všimni si, čo sme nahradili písmenami a, b, c.

Smernicová rovnica priamky

Opäť ďalší spôsob, ako vyjadriť priamku. Tentoraz nám rovnica slúži na to, aby sme pre každú x-ovú súradnicu vedeli vypočítať tú y-ovú.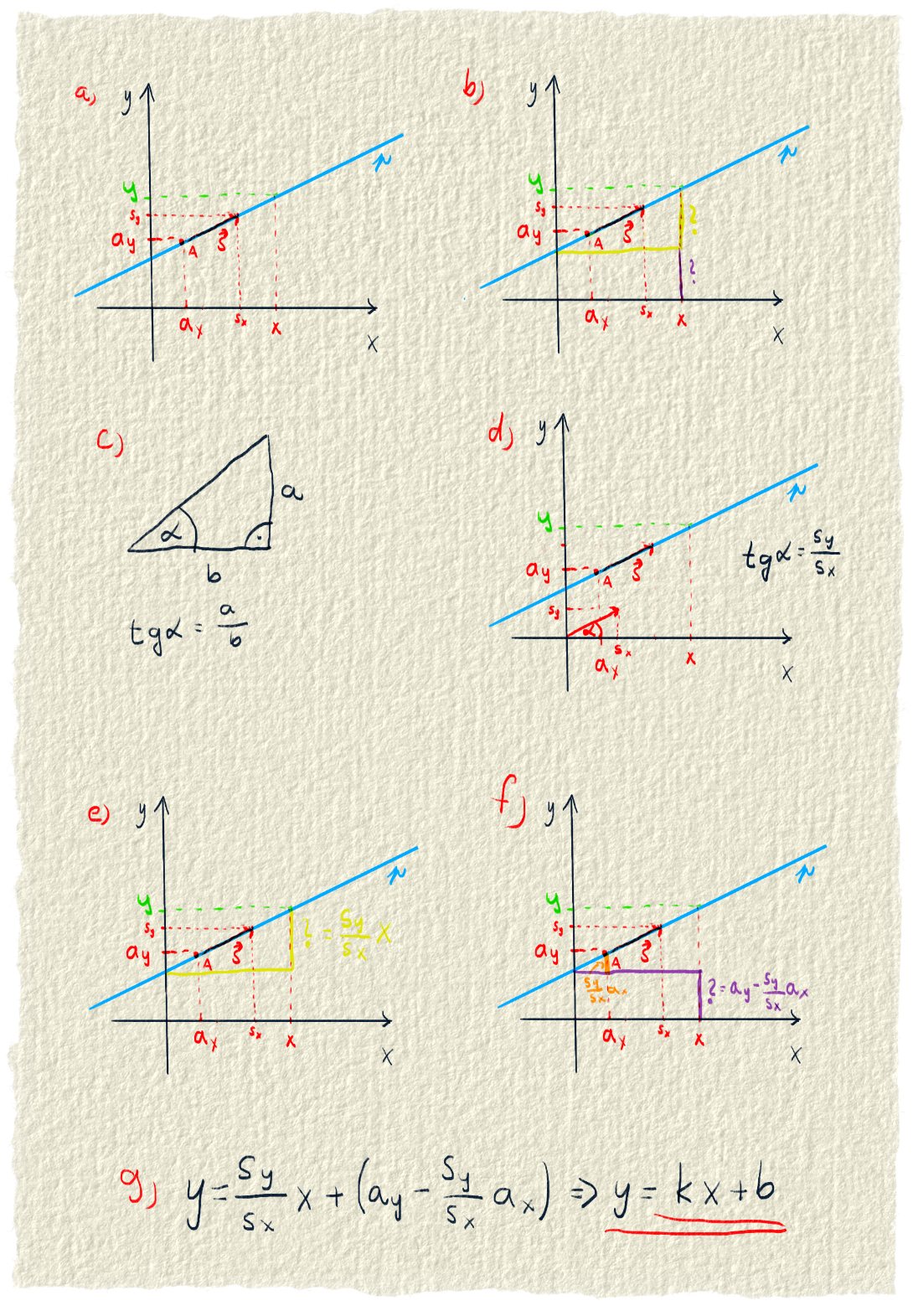

a) Klasika. Poznáme bod A, smerový vektor $\vec{s}$ a teraz už aj x-ovú súradnicu nejakého bodu. Túto súradnicu si môžeš zvoliť akúkoľvek. Vypočítať chceme jeho y-ovú súradnicu.

b) Súradnicu na osi y si vieme rozdeliť na dve časti. Na žltý a fialový otáznik. Bude sa nám ľahšie počítať, pretože práve dĺžku týchto dvoch úsekov vieme dostať z toho, čo poznáme. Všimni si, že predel medzi žltou a fialovou je práve v mieste, kde priamka pretína os y.

c) Pred tým, než sa pustíme do počítania, musíme si zopakovať definíciu tangensu. Budeme ju potrebovať. Pre nás je dôležité, že keď poznáme tangens uhla a jednu stranu, vieme dopočítať stranu druhú.

d) $tg(\alpha)$ je pomer protiľahlej odvesny ku priľahlej. My vieme pomer dostať zo súradníc smerového vektora. Tento pomer hovorí o tom, ako veľmi priamka stúpa. Keď bude rásť strmo, y súradnica smerového vektora bude väčšia ako x-ová. Naopak, keď priamka pôjde mierne, väčšia je x-ová súradnica.

e) Už máme všetky poznatky, ktoré treba a môžeme ísť počítať. Začneme žltým otáznikom. Chceme dostať dĺžku protiľahlej odvesny (to je tá strana, pri ktorej je otáznik). Poznáme $tg(\alpha)$ a poznáme aj dĺžku priľahlej odvesny. Je to súradnica x. Za pomoci poznatku o tangense (bod c) vieme vypočítať dĺžku žltého otáznika: $\frac{s_y}{s_x}x$

f) Tu dopočítame dĺžku fialového otáznika. Zoberieme y-ovú súradnicu bodu A, ale musíme od nej odpočítať časť od priesečníka priamky s y osou nahor. V obrázku je vyznačená oranžovou farbou. Oranžovú časť dostaneme podobne ako žltý otáznik. Z $tg(\alpha)$ a x-ovej súradnice bodu A. Oranžová čiara má dĺžku $\frac{s_y}{s_x}a_x$. Fialový otáznik má teda veľkosť $a_y-\frac{s_y}{s_x}a_x$

g) Už len spočítame fialový a žltý otáznik a máme y-ovú súradnicu bodu X: $y=\frac{s_y}{s_x}x+a_y-\frac{s_y}{s_x}a_x$. Pre lepšiu čitateľnosť nahradíme tie škaredé zlomky písmenami. Dostali sme $y=kx+b$. Písmeno k sa nazýva smernica a hovorí o tom, ako veľmi priamka rastie. Písmeno b zas hovorí o posunutí priamky na osi y. Stavím sa, že si niečo podobné už videl. Rovnaký predpis má aj lineárna funkcia. Je to preto, lebo aj lineárna funkcia je vlastne priamka, na ktorej hľadáš y-ové súradnice k tým x-ovým.

Smernicový tvar rovnice priamky vieme samozrejme odvodiť aj od všeobecnej rovnice priamky. Dosiahneme to tak, že osamostatníme y.

Záver

Priamka je daná dvomi bodmi. Vieme z nich spraviť smerový vektor. Prehodením súradníc a doplnením mínuska k jednej z nich dostaneme zo smerového vektora normálový vektor. Normálový vektor je kolmý na priamku.

Priamku vieme vyjadriť tromi spôsobmi. Prvý spôsob je parametrická rovnica priamky. K bodu, ktorý poznáme sa pripočíta smerový vektor. Jeho ľubovoľným naťahovaním (pomocou parametra t) vieme dostať každý bod na priamke.

Druhý spôsob je všeobecná rovnica priamky. Používame ju vtedy, keď chceme zistiť, či bod patrí na priamku alebo nie. Rovnica funguje tak, že zo zisťovaného bodu a z bodu, ktorý poznáme spravíme vektor. Zoberieme normálový vektor a spravíme s týmto vektorom skalárny súčin. Ak sú vektory na seba kolmé, bod leží na priamke.

Tretí spôsob je smernicová rovnica priamky. Tu poznáme smernicu k, ktorá hovorí o tom, ako veľmi priamka rastie. Písmeno b zasa o tom, ako je priamka posunutá na osi y. Vďaka tomu vieme pre každé x vypočítať jeho y-súradnicu. Smernicovou rovnicou je zapísaná aj lineárna funkcia.