Ako vznikla goniometria

Goniometria taká, ako ju poznáme dnes sa vyvíjala zhruba tri tisícročia. Opísať to všetko, by bolo nadlho. Preto si radšej históriu trošičku upravíme a celý vývoj scvrkneme. Na pochopenie to stačí.

Upravená história začína. Náš príbeh bude začínať jedného pekného dňa, dajme tomu, v strednej ríše v Egypte (to je vtedy, keď stavali pyramídy). V ten letný deň bolo neobyčajne krásne počasie. Slnko svietilo, ale vzduch bol stále svieži. Od mora pofukoval jemný vánok a ani kobylky neotravovali tak, ako zvyčajne. Tunajší slávny architekt Raachef sa opaľoval na dvore. Príjemné popoludnie mu pokazil posol od faraóna. Chceli po ňom, aby panovníkovi postavil parádnu hrobku. Mala to byť najvyššia pyramída v celej egyptskej ríši. Sľúbili mu, že ak sa to podarí, vyvážia ho zlatom. Keď sa nepodarí, dajú ho zožrať krokodílom. Vďaka skvelej motivácií sa Raachef ihneď pustil s chuťou do práce.

Na začiatku ho čakala ohromne ťažká úloha, ale spomienka na krokodílov ho presvedčila, že netreba dlho otáľať. Bolo treba zistiť, ktorá pyramída je najvyššia a potom spočítať rozmery novej pyramídy. Zapálil si oheň, spravil si kávu a pustil sa do práce.

Raachef dlhými krokmi premeriaval svoju nádhernú vilu pri Níle. Popri odháňaní komárov sa pokúšal prísť na to, ako zistí, koľko meria najvyššia pyramída. Nemohol si dovoliť postaviť nižšiu.

Že by ju odmeral? Ale ako, keď nevedel lietať? Nuž, musel si pomôcť inak. Jediné, čo mohol odmerať zo zeme bola šírka pyramídy a uhol, ktorý zvierala so zemou.

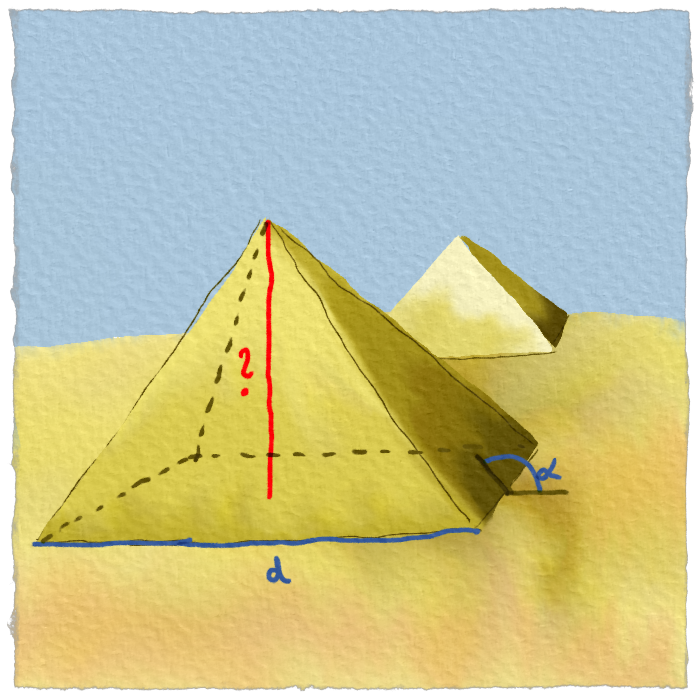
Na pyramíde sa dá zmerať jej šírka, dĺžka a uhol, ktorý zviera so zemou. — Obr. 1.: Raachef potreboval odmerať výšku pyramídy, ale zo zeme dokázal zmerať len šírku pyramídy a uhol ktorý zviera so zemou.

Všimol si, že mu tam vzniká pravouhlý trojuholník. Vidíš ho aj ty? Pozri na obrázok hore. Dole nepozeraj, tam je riešenie.

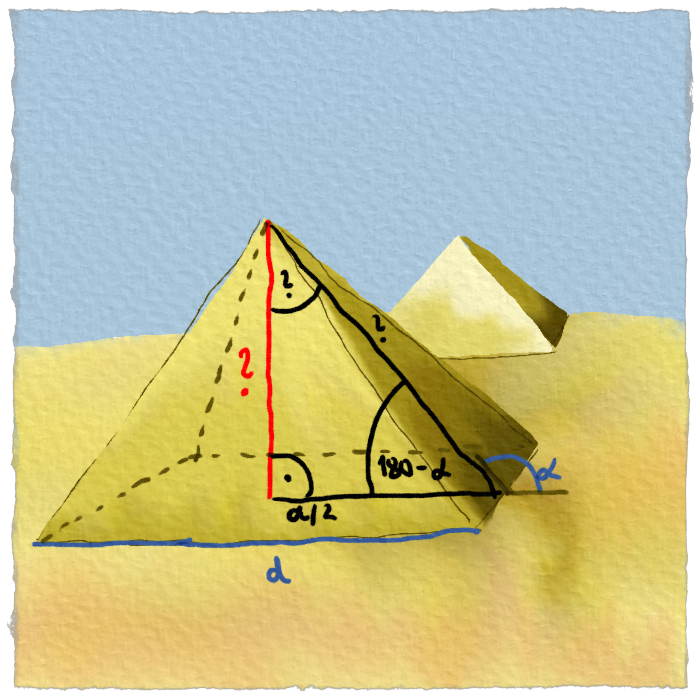
Treba dopočítať výšku pyramídy. — Obr. 2.: Raachef dostal pravouhlý trojuholník, ale stále poznal len jednu stranu a jeden uhol.

Náš architekt stále poznal len sklon (uhol) a šírku pyramídy. Nie je to málo na to, aby vypočítal všetko ostatné?

Raachef dostával strach, že sa skôr stane dobrou večerou, ako dobrým architektom. Kreslil si ten nešťastný trojuholník stále dookola, keď mu náhle udrela do očí jedna vec, ktorú si predtým nevšimol.

Či trojuholník nakreslil veľký alebo malý, pomery jeho strán boli stále rovnaké.

UPOZORNENIE: NA OBRÁZKOCH 3 A 4 SME DĹŽKY STRÁN ZAOKRÚHĽOVALI NA DVE DESATINNÉ MIESTA, TAKŽE KEĎ SI TO BUDEŠ CHCIEŤ PREPOČÍTAŤ, NEMUSÍ TI TO VYJSŤ PRESNE TAK, AKO NÁM.

Pomery strán v pravouhlom trojuholníku. — Obr. 3.: Tu sú dva trojuholníky. Každý z nich má inú veľkosť strán, ale uhly majú rovnaké. Vyrátali sme všetkých 6 pomerov strán a ako si môžeš všimnúť, pre oba trojuholníky sú rovnaké.

Chcel si to overiť. Začal kresliť aj iné trojuholníky. Zasa. Všetky trojuholníky s rovnakými uhlami mali pomery strán stále rovnaké, či boli malé alebo veľké. Naše staré mamy hovoria, že je lepšia raz skúsiť, ako sto-krát vidieť, tak tu je niekoľko trojuholníkov a prepočítaj si ich pomery strán, aby si to zažil na vlastnej koži.

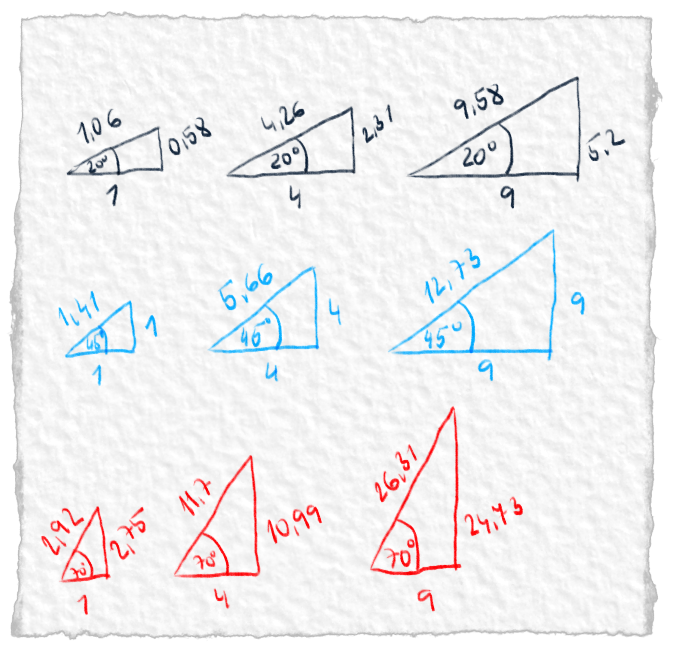
Pomery strán na prepočítanie — Obr. 4.: Skús si prepočítať pomery strán zopár trojuholníkov. Uvidíš, že tie, čo majú rovnaký uhol, budú mať aj rovnaké pomery strán.

Nuž naozaj. Pravouhlé trojuholníky s rovnakými uhlami mali vždy rovnaký pomer strán. Pomery sedeli, nech menil ich veľkosť akokoľvek. Zmenili sa iba vtedy, keď zmenil uhly v trojuholníku

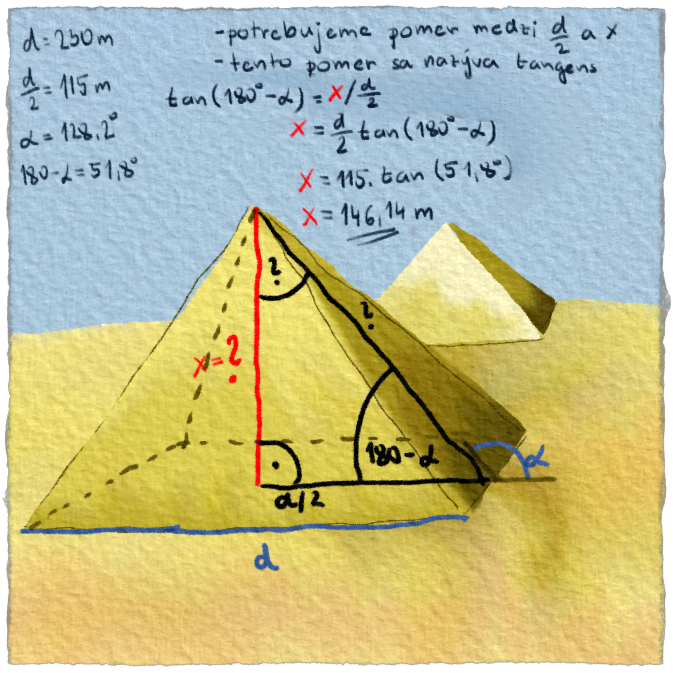
To mu pomohlo. Keď pre uhol vedel, aký je pomer strán, mohol si dovoliť jednu stranu nevedieť. Dopočítal ju z jednoduchej rovnice. Predstava krokodílov sa vzdialila. Poznal niektoré uhly a poznal niektoré strany. Zvyšok už dopočítať vedel. Zvládol by si prísť na rovnicu aj ty alebo by ťa zožral krokodíl? Skús sa trochu zamyslieť ;). Na obrázku dolu je riešenie.

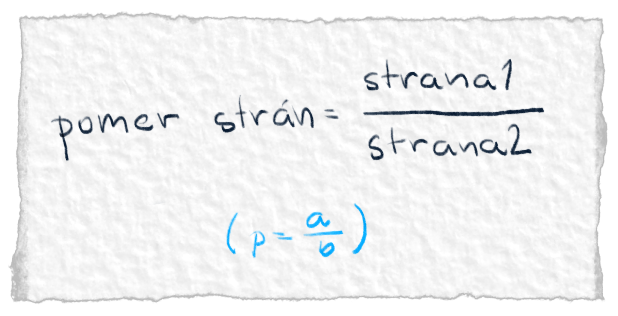
Pomery strán - rovnica — Obr. 5.: Rovnica, z ktorej vieme dopočítať jednu zo strán, ak poznáme pomer strán pre daný uhol.

Raachef vedel, že sa o jeho objave bude učiť v školách, tak chcel narobiť deťom trochu problémov. Pomery nazval čudnými menami: sínus, kosínus, tangens, kotangens, sekans a kosekans . Takže ak nabudúce nebudeš vedieť, čo tieto slová znamenajú, sú to jednoducho pomery strán v pravouhlom trojuholníku.

Názvy pomerov strán - goniometrické funkcie — Obr. 6.: Názvy a označenia pomerov strán: **sin - sínus, cos - kosínus, tan - tangens, cotg - kotangens, sec - sekans, csc - kosekans**

Po objavení tejto úžasnej myšlienky, Raachef už ľahko dopočítal výšku pyramídy. Vedel by si to aj ty? Pravouhlý trojuholník je k dispozícií na obrázku č. 2. Poznáš jednu stranu a jeden uhol - sú nakreslené čiernou. Ak ti nechýba abstraktné myslenie, stačí napísať vzorec. Ak potrebuješ čísla, môžeš uvažovať, že dĺžka pyramídy je 230 metrov (polku dĺžky snáď vypočítať vieš) a uhol alpha je 128,2° (spraviť 180-128,2 vieš hádam tiež)[1]. Riešenie je dole na obrázku:

Počítanie výšky pyramídy — Obr. 7.: Výška najvyššej pyramídy v Egypte je 146 metrov. Môžeš si overiť na nete.

Zhrnutie

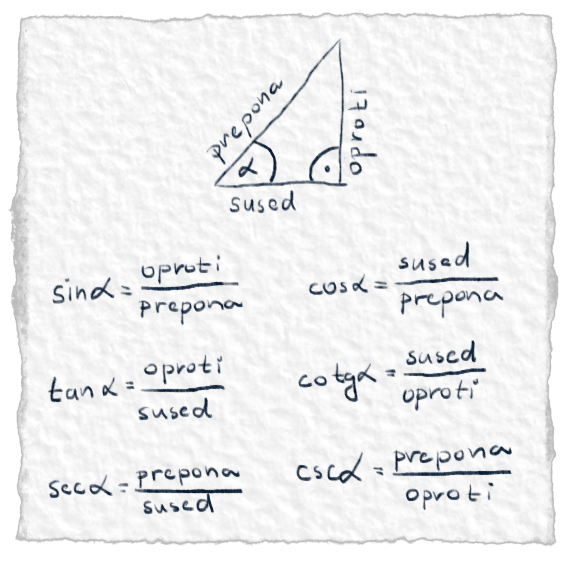
Sínus, kosínus, tangens, kotangens, sekans, kosekans sú mená pre pomery strán v pravouhlom trojuholníku. Pre každý uhol je iný pomer strán. Pre jeden uhol je pomer strán rovnaký, nezávisle od toho, ako je trojuholník veľký. Keď poznáme pomer, stačí nám poznať len jednu stranu a druhú dopočítame.

Zdroje

[1] Dimensions of the Cheops-pyramid (Khufu's pyramid). https://www.cheops-pyramide.ch/khufu-pyramid/khufu-numbers.html