Miery polohy

Miery polohy hovoria o polohe údajov na číselnej osi. Sú to čísla, ktoré vhodne reprezentujú údaje. K mieram polohy patrí modus, kvantily a stredná hodnota. Stredná hodnota môže byť buď medián alebo priemer.

Vďaka mieram polohy vieš, v akých číslach sa ti pohybujú údaje bez toho, aby si si ich musel všetky prečítať. Napríklad ak priemer cien bytov je 90 000 eur, nemusíš poznať všetky ceny bytov, aby si vedel, že ceny bytov sa pohybujú v desiatkach tisíc. Keď meriaš teploty v januári, priemer ti vyjde možno -5℃. Vieš, že teploty sa budú pohybovať niekde v mínusových číslach.

Miery polohy vedia odhaliť aj nejaké nepresnosti. Napríklad meriaš veľkosť bacilov. Priemerne budú merať 400nm. Keď nameráš päť metrového bacila, vieš, že si niekde spravil chybu. Využiť to môžeš napríklad, keď si chceš porovnať plat. Budeš pracovať ako čašník a na internete zistíš, že priemerná hrubá mzda v tvojom obore je nejakých 850 eur. Keď dostaneš aj ty mzdu niekde okolo 850 eur, vieš, že je to na poriadku. Keď dostaneš nejakú veľkú, napríklad 5000 eur, tak je to dosť ďaleko od strednej hodnoty a ty vieš, že šéf si ťa extrémne váži. Keď dostaneš 200 eur, vieš že treba hľadať iné zamestnanie.

Priemer

Priemer snáď poznáš zo základnej školy, takže vysvetlením by sme ťa mohli len pomýliť :D. Pre tých, čo sa vyhli základnej škole je priemer prostredná hodnota medzi údajmi. Nemusí to byť priamo hodnota niektorého z údajov. Priemer je vypočítaný z dát. Zo všetkých čísiel na svete je to číslo, ktoré je najbližšie ku každému údaju.

Používame ho vtedy, keď chceme vedieť v akých číslach sa pohybujú údaje. Keď máme údaje o cenách bytov, tak priemer bude napríklad 90 000 eur a my vieme, že ceny bytov sa pohybujú v desiatkach tisíc eur. Keď máme údaje o cenách potravín, tak priemer bude napríklad 4 eurá a vďaka tomu vieme, že za potraviny platíme pár eur. Pomocou priemeru vieme porovnať dáta o rovnakých veciach. Napríklad pomocou priemeru môžeme porovnať ceny bytov v Bratislave, Kysuckom Novom Meste a v Prešove. Nemôžeme však už porovnávať rôzne veci. Ceny rožkov s cenami bytov by sme porovnali ťažko. Tiež aj priemerné ceny bytov s priemernou teplotou v januári by sa porovnať nedali.

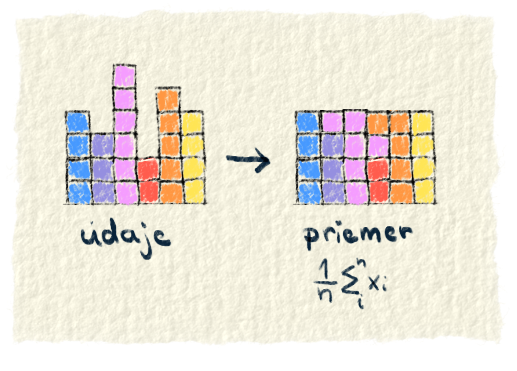
Matematika by nebola matematikou, keby aj na výpočet priemeru neexistoval nejaký všeobecný zápis. Je to tento peknučký vzorček: $$ \overline{x}=\frac{1}{n}\sum_{i=1}^n x_{i} $$ Písmeno x označuje dáta. Pre nás je to overall hráčov. $\overline{x}$ označuje priemer z dát. Konkrétne priemer značí tá palička nad x-kom. Takže odteraz keď budeš vidieť paličku nad nejakým písmenom, budeš vedieť, že je to priemer. Ďalej tam je $\frac{1}{n}$. Písmeno n označuje počet dát, z ktorých sa ráta priemer. Možno si si už za svojho pôsobenia vo vzdelávacom systéme všimol, že keď násobíš zlomkom $\frac{1}{n}$, tak vlastne delíš n-kom. Ďalej je tam $\sum_{i=1}^n x_{i}$. Tým spočítaš všetky dáta. Pre nás to znamená zrátanie overall hráčov. Ak nevieš ako funguje suma, je to vysvetlené tu. Zhrnutie vzorca je také, že zrátaš všetky dáta a vydelíš ich ich počtom.

Priemer z hráčov Inter Milano vyrátame takto: Zázrak dostať z takého vzorca výsledok, že? Nie je to však nič zložité, v hlave (na kalkulačke) rátaš normálne (suma je len kratší zápis):

Keď sa ráta priemer, údaje sa v podstate pekne zarovnajú. Ten čo má viac dá tomu, čo má menej. To čo trčí sa zarovná a to čo má málo, tam sa pridá. Výsledok je stred medzi údajmi.

Medián

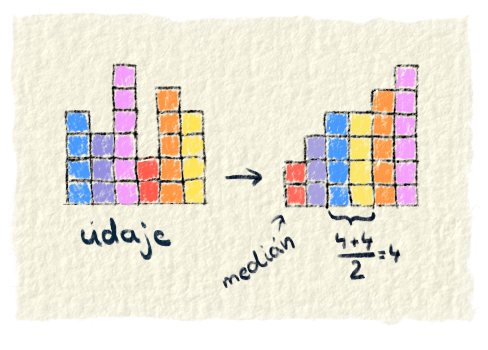
Medián je prostredná hodnota z údajov. Keď sú údaje zoradené od najmenšieho po najväčší, tak medián je v strede, napr. pri piatich údajoch je medián tretí údaj. Keď je údajov párny počet, tak medián je priemer z prostredných dvoch. Napríklad pri šiestich údajoch sa zoberie tretí a štvrtý údaj. Spočítajú sa a predelia dvomi (spraví sa priemer). Výsledok je medián.

Medián rozdeľuje údaje na dve polovice. Na tú, kde sú údaje s menšími hodnotami ako medián a na tú, kde majú údaje väčšie hodnoty ako medián.

Medián sa označuje podobne ako priemer, len miesto čiarky je vlnovka. Pre údaje označené písmenom x je medián $\tilde{x}$.

Pre Inter Milano je medián šiesty hráč. Je to Stefan de Vrij s overallom 84. Ak by sme napríklad niekde zapatrošili futbalistu Nicolò Barellu, tak by sme medián museli rátať z desiatich hráčov. Zobrali by sme si prostredných dvoch. Sú to Stefan de Vrij a Mauro Emanuel Icardi Rivero. Z ich overallov by sa vyrátal priemer: (84+85)/2 = 84,5. Medián by bol potom 84,5.

Kvantil

Prišiel si pozrieť na tréning svojho tímu a vidíš, že futbalistom sa veľmi nechce. Chceš ich motivovať. Rozdelíš ich do dvoch skupín podľa overallu. Horšia skupina bude nosiť na ihrisko lopty, lepšia nie.

Aby hráč vedel, do ktorej skupiny patrí, potrebuje vedieť overall, ktorý oddeľuje horších od lepších. Zoradíš si hráčov podľa overallu a vyberieš prostredného. Hráč, ktorý má menší overall ako prostredný, patrí k horším, ten čo má väčší, patrí k lepším.

Ak by bol tvoj tím Inter Milano, tak prostredným hráčom bude Samir Handanovič. Tí čo majú menší alebo rovnaký overall, sú horší, tí čo majú väčší, patria do lepšej skupiny. Možno si si všimol, že sme vlastne vypočítali medián Inter Milano.

Overall hráča, ktorý oddeľuje skupiny napíšeš niekde na nástenku a už všetci budú vedieť, či majú nosiť lopty alebo nie.

Zavolá ti sponzor a ponúkne, že tretine futbalistov zaplatí wellness. Použiješ ho ako odmenu. Teraz už máš tri druhy odmien. Prvá je wellness+nenosenie, druhá je nenosenie a tretia je nosenie všetkých vecí na ihrisko. Rozdelíš teda hráčov do troch skupín. Zoradíš ich od najhoršieho po najlepšieho a nájdeš hráčov, ktorí delia tím na tri skupiny. Ich overally zasa napíšeš na nástenku a všetci budú vedieť, čo sa ich týka. Pre Inter Milano by boli títo hráči Lukaku a Martinéz, lebo delia tím na tri skupiny.

Futbalistov, ale aj iné údaje, môžeš rozdeliť na koľko skupín chceš. Údaje, ktoré oddeľujú skupiny sa nazývajú kvantily.

Keď máš 11 hráčov, tak tých čo rozdelia údaje na skupiny nájdeš ľahko. Pre 18 000 by si sa niečo nahľadal. Veľké množstvá údajov vyžadujú inteligentnejšie riešenie ako je čítať riadok za riadkom.

Keď sme delili hráčov na dve skupiny, kvantil bol hráč na pozícií v strede. Hráči, ktorí oddeľovali tri skupiny sa nachádzali na konci prvej a druhej tretiny údajov. Keď chceme vo všeobecnosti vypočítať kvantily (údaje, ktoré oddeľujú ostatné údaje) potrebujeme vedieť pozíciu, na ktorej sa nachádzajú.

Recept na výpočet pozície údaju začína tým, že údaje zoradíme od najmenšieho po najväčší. Pozíciu vypočítame z veľkosti údajov a z časti, v ktorej sa kvantil nachádza (či je napríklad v polovici, prvej tretine, štvrtej jedenástine atď.). Časť v ktorej sa nachádza vyjadríme klasicky zlomkom (koľká časť delená počtom častí). Veľkosť údajov si označíme N, počet častí bude označený písmenom q, ktorý kvantil počítame bude k a výsledná pozícia bude P. Takto vypočítame pozíciu, na ktorej sa kvantil nachádza. $$ P_k = \frac{k}{q} * (N+1)$$ Samotný kvantil je údaj na tejto pozícií (pre nás je to overall hráča). Kvantil označíme písmenom Q. To malé k znamená poradové číslo kvantilu. $$ Q_k = x_{p_k}$$ Vo vzorci na vypočítanie pozície kvantilu sa k počtu údajov pripočítava 1. Dôvod ti ukážeme na príklade 11 futbalistov. Chceme z nich vypočítať pozíciu hráča, ktorý rozdeľuje údaje na polovicu. Keď si to spočítaš na prstoch, tak je to šiesty hráč. Ak by sme dali len 0.5*11, tak výsledok je 5,5. Keď dáme 0.5*12, výsledok je 6.

Počítanie pozície iba z počtu hráčov N a nie z N+1, vždy vráti výsledok trochu menší ako má byť. Keď sa tam pričíta 1, vyjde to presne. Toto platí pre akýkoľvek počet údajov a pre akúkoľvek časť údajov (napríklad aj pre druhú tretinu z jedenástich hráčov). Môžeš si to vyskúšať na viacerých príkladoch, ale tie si musíš vymyslieť sám.

Teórie bolo zatiaľ dosť, poďme na príklad. Chceme si rozdeliť hráčov Interu Milano na tri časti podľa overall.

Hráčov chceme deliť na tri časti, teda počet častí q bude 3. Kvantily budú dva (vždy keď niečo delíš na časti, tak hraníc medzi časťami je o jednu menej ako častí). Písmeno k, ktoré označuje poradie kvantilu bude nadobúdať hodnoty 1 a 2. Počet dát N bude v našom prípade 11. Pozíciu sme rátali pre dva kvantily. Prvý kvantil vyšiel na pozícií 4 a druhý na pozícií 8. Kvantily sú teda čísla 81 a 85.

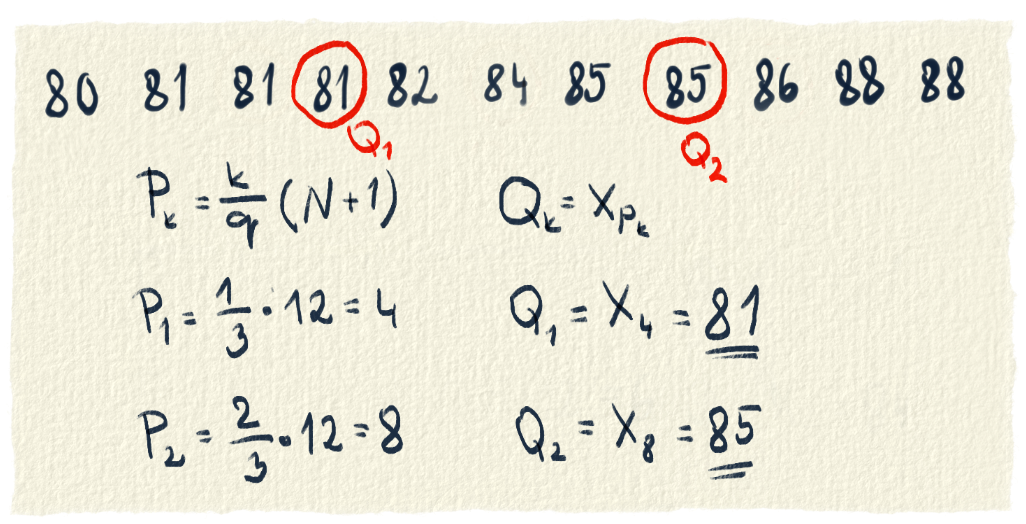
Keď sa ti stane taká vec, že kvantil nevyjde presná pozícia, ale nejaké desatinné číslo, tak ho zaokrúhliš raz nadol a raz nahor. Zoberieš údaje z týchto dvoch pozícií a spravíš z nich priemer. Kvantil bude niekde medzi týmito dvomi číslami. V tomto príklade sme pridali dvanásty overall:

Vráťme sa k motivovaniu hráčov. Futbalisti, ktorých overall je horší alebo rovný ako 81.5 musia nosiť na ihrisko všetky veci. Tí, ktorých overall je lepší ako 81.5 a zároveň horší alebo rovnaký ako 85.5, nemusia na ihrisko nosiť nič. Tí, čo sú lepší ako 85.5, nemusia na ihrisko nosiť nič a ešte k tomu idú aj na wellness.

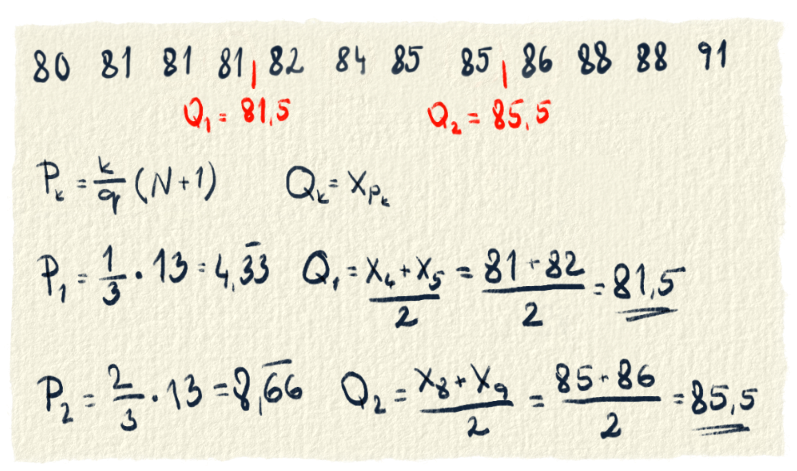
Ešte máme s kvantilmi jeden problém. Možno si si všimol, že ak by sme Inter Milano rozdelili na štyri časti, tak prvý kvantil by bol na treťom mieste. Tam je hodnota 81. Ale aj na druhom a štvrtom mieste je hodnota 81. Toto je ten problém. Keď ako kvantil určíme číslo 81, neplatí, že štvrtina hodnôt bude menšia alebo rovná ako 81. To, že kvantil nám vyjde jedna z rovnakých hodnôt, sa nevyskytuje našťastie veľmi často. Ak sa to už stane, býva to vtedy, keď je dát málo. To je aj náš prípad. Tento problém sa dá vyriešiť tak, že kvantil vyrátaš vzorcom, ktorý používaš a výsledok prehlásiš za správny, aj keď budú okolo kvantilu rovnaké hodnoty. (Chceli by sme upozorniť na dve slová "ktorý používaš", pretože kvantil sa dá vypočítať viacerými spôsobmi.) My by sme teda povedali, že 25%-tný kvantil je 81. [1]

Údaje môžeš deliť na hocikoľko častí chceš. Ľudia však najčastejšie rozdeľujú dáta iba na nejaké časti. Tieto rozdelenia dostali aj svoje názvy. Sú to:

• Medián - delí dáta na dve časti
• Tercil - delí dáta na tretiny (tercil sme počítali v príklade pre Milano)
• Kvartil - delí dáta na štvrtiny
• Decil - delí dáta na desatiny
• Percentil - delí dáta na stotiny

Keď počítaš hocijaký kvantil, časť, v ktorej sa nachádza je $\frac{k}{q}$. Toto ti vyjde desatinné číslo. Keď to vynásobíš číslom 100, dostaneš to v percentách. Aby ľudia vedeli, o ktorých kvantiloch sa rozpráva, pomenovali ich podľa percent. Napríklad údaje delíš na štyri časti a chceš tretí kvantil. Zlomok $\frac{3}{4}$ vyjde 0,75. Po vynásobení 100 je to 75%. Tento kvantil sa nazýva 75 percentný kvantil. Keď delíme údaje na 88 častí a chceme kvantil číslo 66, dostaneme $\frac{66}{88}*100=75$. To je zasa 75% percentný kvantil. Keď delíme údaje na 30 častí a chceme trinásty kvantil, dostaneme $\frac{13}{30}*100=43,333$. Tento kvantil nazývame 43,333 percentný kvantil. Takýchto príkladov na pomenovanie si môžeš vymyslieť veľa.

Ak sa ti doteraz toto všetko zdalo neznáme ver, že si sa už s kvantilmi stretol. Táto pamätná chvíľa nastala, keď si ukončil deviaty ročník základnej školy testom nazývaným monitor. Keď vám prišli výsledky, určite si sa so spolužiakmi porovnával, kto má lepší percentil. Ak si mal z matematiky percentil napríklad 68, znamená to, že si lepší ako 68% deviatakov na Slovensku.

Modus

Modus je najpočetnejšia hodnota z údajov. Spočítajú sa rovnaké údaje a tých, ktorých je najviac, tak to je modus.

Pre Inter je hodnota 88 dva razy, 86 raz, 85 je dva razy, 84 a 82 sú po jednej, 81 je tri razy a 80 iba raz. Najviac je hodnoty 81, lebo sa vyskytuje v dátach tri razy. Modus je teda 81.

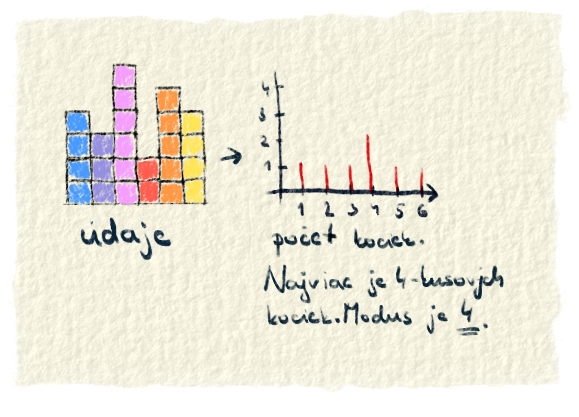
Zdroje