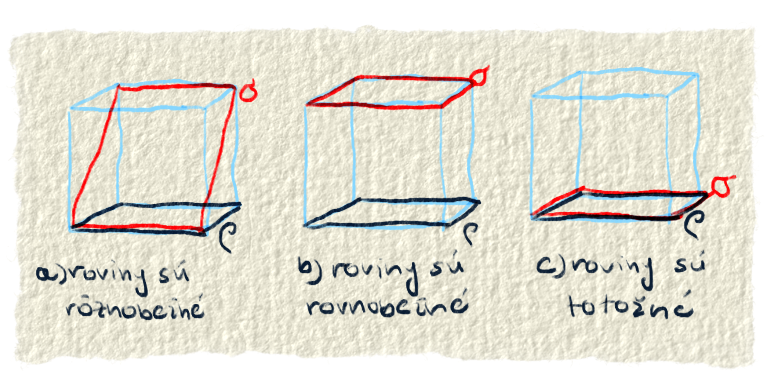
Vzájomná poloha rovín

Dve roviny môžu ležať na sebe, vtedy sú totožné. Keď ležia nad sebou, sú rovnobežné. Roviny, ktoré sa pretínajú, sú rôznobežné.

Pozri sa na obrázok č. 1 a skús povedať, koľko spoločných bodov majú rovnobežné roviny, koľko rôznobežné a koľko totožné.

Vzájomná poloha dvoch rovín — Obr. 1.: Roviny môžu byť rovnobežné, rôznobežné alebo totožné.

Vzájomnú polohu rovín vieme určiť pomocou ich všeobecných rovníc. Budeme sa pýtať, koľko bodov majú roviny spoločných. Keď z rovníc vyjde, že nemajú žiaden spoločný bod, tak sú rovnobežné. Keď výsledok povie, že majú nekonečne veľa spoločných bodov, tak sú totožné. Keď sú roviny rôznobežné, výsledkom je priamka. Ako si si na obrázku č. 1 určite všimol, rôznobežné roviny sa pretínajú a ich prienikom je priamka.

Poďme sa pozrieť na to, ako vypočítame vzájomnú polohu rovín.

Potrebujeme všeobecné rovnice rovín, ktoré chceme počítať.
Dáme si ich pod seba a počítame ako sústavu rovníc.
Tešíme sa z výsledku.

Výsledok môže byť všelijaký. Napríklad môžu vypadnúť všetky premenné a výsledok bude, že nula sa rovná nule. To znamená, že za premenné môžeme dosadiť hocijaký bod, ktorý patrí jednej rovine a on bude patriť aj tej druhej. Z toho nám vyplýva, že roviny sú totožné.

Pri rovnobežných rovinách nám zasa vypadnú všetky premenné, ale na každej strane rovnice bude iné číslo. To znamená, že na tomto svete neexistuje jeden jediný bod, ktorý patrí obom rovinám.

Ostali nám roviny rôznobežné. Pri nich nevypadnú premenné, ale vieme ich vyjadriť. Môže sa zdať, že tu máme problém, lebo máme dve rovnice a tri neznáme. Čiže dve premenné musíme vyjadriť pomocou tej tretej. To je to, čo práve chceme, pretože dostaneme parametrickú rovnicu priamky a ešte na začiatku sme si povedali, že prienikom dvoch rovín je priamka.

Príklad - roviny sú rôznobežné — Obr. 2.: Máme všeobecné rovnice dvoch priamok. Dáme ich do sústavy a snažíme sa vyjadriť y. To sa aj podarilo, y vyšlo, že *y = -9 -17z*. Dosadíme to za x a dostaneme, že *x = -13 -26z*. Ešte to tam kazí z až do chvíle, kým si uvedomíš, že z môžeme použiť ako parameter.

Ešte si vypočítame dve sústavy rovníc.

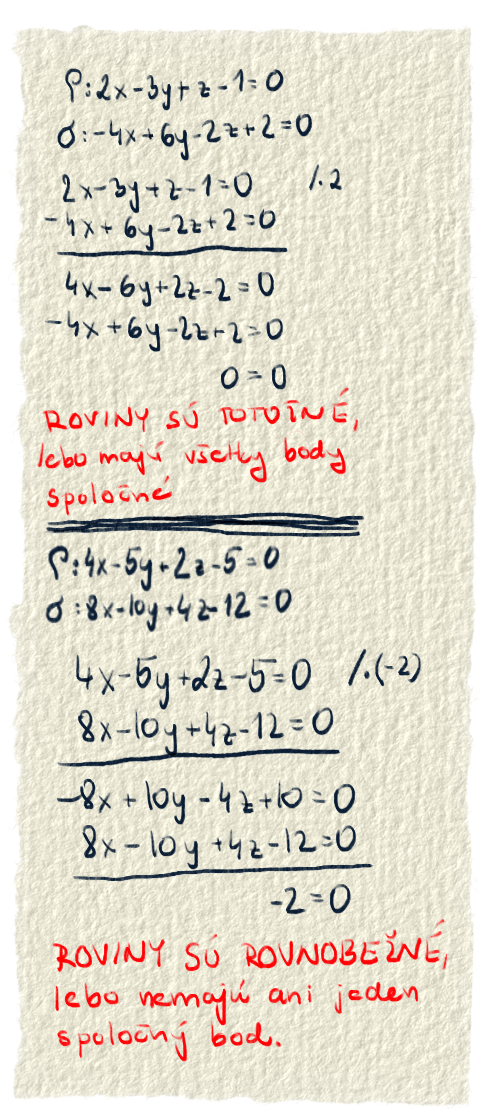
Dva príklady. Prvý - roviny sú totožné. Druhý - roviny sú rovnobežné. — Obr. 3.: V prvej sústave nám vypadli všetky premennú dostali sme *0 = 0*. To je prípad, kedy sú roviny totožné. V druhej sústave zasa vypadli všetky premenné, ale výsledok je *-2 = 0*. Znamená to, že roviny sú rovnobežné.

Dôvod, prečo rovnice fungujú

Ak ťa trápi otázka, prečo tie výpočty fungujú, si tu na správnom mieste. Aspoň trochu sa ti pokúsime objasniť kúzla skryté v rovniciach 😀.

Najprv si v skratke povieme, čo je to všeobecná rovnica roviny. Ak chceš vedieť o nej viac, prečítaj si toto. Všeobecná rovnica roviny má tvar ax+by+cz+d=0. Ako si si mohol všimnúť v príkladoch, písmená a,b,c,d sú čísla písmená x,y,z sú neznáme. Písmená a,b,c sú súradnice normálového vektora roviny. Písmeno d je opačná hodnota skalárneho súčinu normálového vektora roviny s nejakým bodom patriacim rovine. Neznáme písmená x,y,z sú súradnice bodu, ktorý patrí rovine. Môžeme použiť akýkoľvek bod, ktorý patrí rovine.

Ďalej potrebujeme vedieť niečo o skalárnom súčine normálového vektora roviny a bodu, ktorý patrí rovine. Robíme teda skalárny súčin normálového vektora roviny a bodu, ktorý patrí rovine. Vieme, že pre všetky body roviny, bude tento skalárny súčin rovnaký.

V rovnici máme dva skalárne súčiny. Prvý je normálový vektor s bodom, ktorý nepoznáme. To je to ax+by+cz. Druhý skalárny súčin je skrytý pod písmenom d. To je skalárny súčin normálového vektora s bodom, ktorý poznáme a vieme, že patrí rovine. Výsledkom skalárneho súčinu je číslo a v tejto rovnici sme ho skryli pod písmeno d. Tieto dva skalárne súčiny sú rovnaké a keď ich od seba odpočítame, musí vyjsť 0. Nech ťa nepletie, že vo vzorci je +d. Matematika už zariadi, že pri čísle bude správne znamienko. Ak za súradnice x,y,z dosadíme bod, ktorý rovine nepatrí, skalárne súčiny nebudú rovnaké. Toľko v krátkosti k tomu, ako funguje všeobecná rovnica roviny. Tu máme napísané viac.

Teraz sa pozrieme na to, ako by sme všeobecnú rovnicu roviny mohli použiť pri určovaní vzájomnej polohy rovín. Vieme, že aby rovnica roviny platila, musíme za x,y,z dosadiť bod, ktorý patrí rovine. Vieme ju teda použiť na to, aby sme zodpovedali otázku, že či bod patrí rovine alebo nie. Už sme si povedali, vzájomnú polohu rovín vieme určiť podľa toho, koľko bodov majú spoločných. Teda koľko nájdeme takých bodov, ktoré patria obom rovinám. Aby sme zistili, či majú roviny nejaké body rovnaké, dáme ich všeobecné rovnice do rovnosti, resp. do sústavy rovníc.

Pri riešení nám môžu vypadnúť všetky čísla a ostane nám, že 0=0. Povedali sme si, že to znamená, že roviny sú totožné. Totožné roviny majú rovnaký smer normálového vektora, aj keď každá ho môže mať inak veľký. Pretože normálový vektor je rovnaký, tak vypadne. Ak majú rovnaké aj všetky body, tak vypadne aj skalárny súčin skrytý pod písmenom d, pretože aj ten je rovnaký pre obe roviny. Ostane 0=0.

Aj pri rovnobežných rovinách je smer normálového vektora rovnaký a preto vypadne. Body však už nie sú rovnaké, skalárny súčin skrytý pod d bude pre každú rovinu iný a preto nevypadne. Na každej strane rovnice bude iné číslo, to znamená, že nikdy nenájdeme taký bod, ktorý bude patriť obom rovinám. Roviny sú rovnobežné.

Pri rôznobežných rovinách dokážeme vyjadriť dve premenné pomocou tretej. Keď použijeme tú tretiu premennú ako parameter, dostaneme parametrickú rovnicu priamky. Keďže sme dostali rovnicu priamky, vieme, že spoločné body rovín ležia na priamke. Teda roviny sa pretínajú a sú rôznobežné. Príklad máme vypočítaný na obrázku č. 2.