Skalárny súčin

Skalárny súčin je jedna z tých novších vecí, ktoré sa objavili v matematike. Na používanie v bežnom živote je to príliš vysoká matematika, preto ho ani nenájdeme priamo medzi nami. Skrýva sa v rôznych veciach, ktoré by bez neho nemohli fungovať, a my si zase nevieme už teraz predstaviť fungovanie bez nich.

Ale pekne po poriadku. Najprv sa pozrieme na to, kedy skalárny súčin vznikol, na čo ho ľudia potrebovali, ako funguje a na čo ho potrebujeme dnes.

Objavenie skalárneho súčinu

Začalo to v roku 1773 pánom pomenovaným Joseph Louis Lagrange. V jeho rodnej reči sa volal Giuseppe Luigi Lagrangia, lebo pôvodom bol Talian. Až neskôr sa dal prerobiť na Francúza. Jeho otec bol v službách kráľa Sardínie, ale aj tak neboli veľme bohatí. Otec totiž prerobil skoro všetky peniaze v nejakých podivuhodných finančných transakciách. Mladý Giuseppe tak bol nútený zanechať myšlienku na štúdium práva a venovať sa nejakému skromnejšiemu povolaniu, čo v tých časoch matematika zjavne bola.

Čo bola pre Giuseppeho smola, pre ľudstvo bolo šťastie. Pri štúdiu tetrahedronu prišiel na niečo, čo sa neskôr vyvinulo do skalárneho súčinu tak, ako ho poznáme dnes. Prišiel aj na veľa iných užitočných vecí, ale teraz sa zameriame na skalárny súčin.[1]

Ako to už v matematike býva, na začiatku nebola podoba skalárneho súčinu taká ako dnes, ale postupne sa kryštalizovala. Jeden pridal to, druhý to, až nakoniec vznikol skalárny súčin. Hamilton sa zaoberal quaterniónmi a spravil skalárny súčin pre ne. Okrem toho zaviedol pojem skalárny súčin a vektor. To bol rok 1843. Neskôr Maxwell použil Hamiltonovu prácu vo svojom elektromagnetizme a skalárny súčin sa tak stal pevnou súčasťou fyziky. Do konca storočia sem tam ešte niekto niečo k skalárnemu súčinu prilepil.

Začiatkom 20.storočia robil David Hilbert a pár jeho kamošov na veci, ktorá sa volá Hilbertov priestor. Je to priestor, kde sa počíta s nekonečne rozmernými vektormi. Zadefinovali tu spôsob násobenia vektorov, ktorý sa nazýva inner product (pardon za anglický názov). Tento inner product je zovšeobecnením skalárneho súčinu. Takže takto sa skalárny súčin dostal do ešte väčšej matematiky, v akej bol.[2]

Čo je to skalárny súčin

Skalárny súčin je niečo, čo môžeme nazvať spoločný účinok dvoch vektorov. Na to, aby sme dostali celkový spoločný účinok, treba vyrátať spoločný účinok po jednotlivých zložkách vektorov a potom to spočítať dokopy. Spoločný účinok v jednom rozmere dostaneme tak, že vynásobíme veľkosť zložiek v danom rozmere.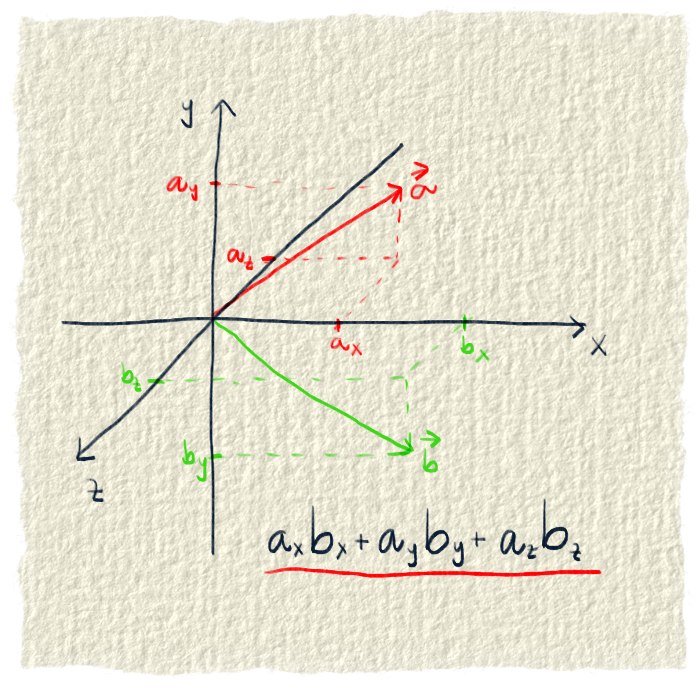

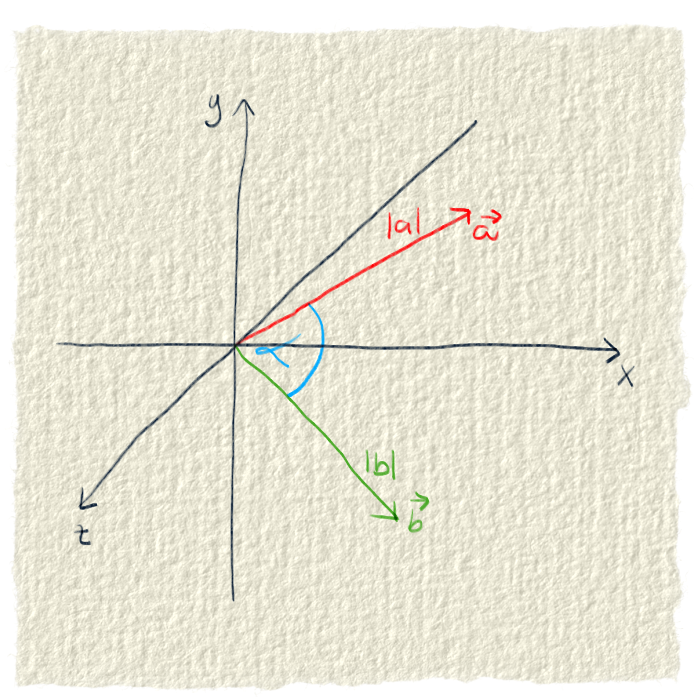
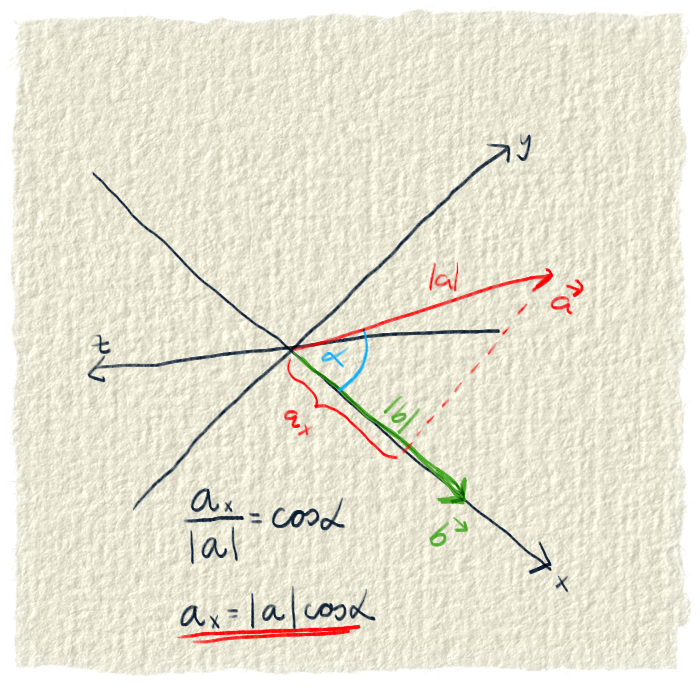
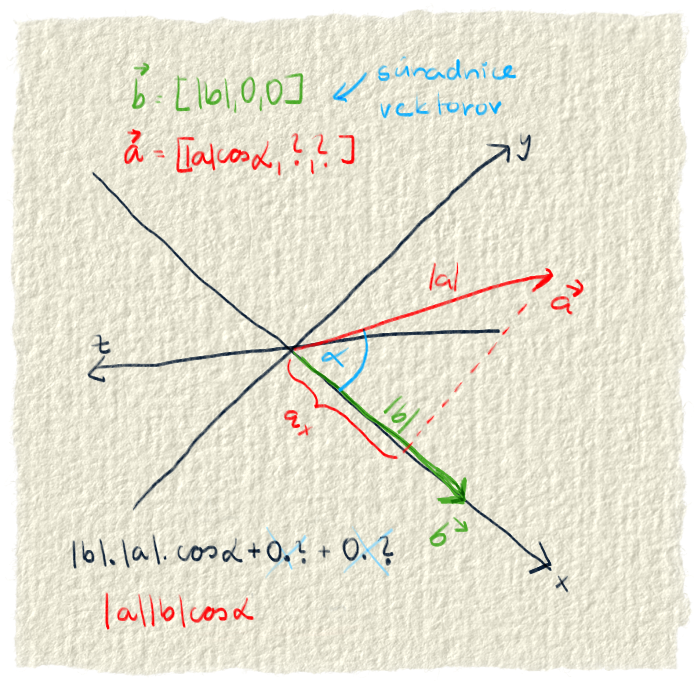
Tento zápis sa nazýva aj algebraický zápis skalárneho súčinu. $$ \vec{u} \cdot \vec{v} = u_{x}v_{x} + u_{y}v_{y}$$ Používa sa vtedy, keď sú známe súradnice vektorov. No nie vždy poznáme práve tie. Niekedy sa môže stať, že sú známe iba veľkosti vektorov a uhol medzi nimi. Vtedy sa tiež dá na tento problém pozrieť tak, že vyrátame spoločné pôsobenie po zložkách a potom to sčítame.

Ale musíme si problém na to prispôsobiť. Problém si prispôsobíme tak, že jeden vektor necháme ísť presne v smere jedného z rozmerov. Jeho veľkosť bude teda veľkosť zložky v tomto rozmere a v ostatných rozmeroch budú zložky nulové.

Potom si zistíme zložku toho druhého vektora, ktorá ide v smere toho prvého. Tú dostaneme tak, že spravíme kolmicu z konca vektora na tú os, kde je ten prvý vektor. Dostávame pravouhlý trojuholník, kde poznáme veľkosť prepony a uhol medzi ňou a priľahlou stranou. Zo vzťahu pre kosínus sa dá odvodiť veľkosť priľahlej strany, čo je vlastne hľadaná zložka vektora.

Ostatné zložky zisťovať netreba, pretože ten prvý vektor ich má nulové a keď sa to spolu vynásobí, tak aj tak dostaneme nulu. Keď už poznáme všetky zložky vektorov, len ich vynásobíme a zrátame.

Dostávame niečo, čo sa volá geometrický zápis vektorového súčinu. Používa sa vtedy, keď poznáme veľkosti vektorov a uhol medzi nimi. $$ \vec{u} \cdot \vec{v} = |\vec{u}||\vec{v}|cos \alpha $$

Výsledok skalárneho súčinu

Výsledok skalárneho súčinu je jedno číslo. Je to preto, lebo sme počítali iba s veľkosťami vektorov a nie so smermi. Dostali sme niečo, čo nám hovorí o tom, ako veľmi dva vektory účinkujú/ťahajú/pôsobia v smere jedného alebo druhého z nich.

Od skutočnosti, že výsledok je iba jedno číslo, je odvodený názov tejto operácia - skalárny súčin. Pretože slovo skalár označuje veličinu zadanú iba jedným číslom - skalárom.

Keď výsledok vyjde 0, znamená to, že vektory sú na seba kolmé a teda ani trochu si navzájom nepomáhajú. Záporné číslo hovorí o tom, že ťahajú opačnými smermi.

Skalárny súčin sám o sebe nemá žiaden význam. Dáva mu ho až jeho použitie.

Je to ako pri obyčajnom násobení. 10*20 = 200 nemá žiaden význam. Až keď povieme, že máme 10 debničiek, v každej je 20kg jabĺk a spolu máme 200kg jabĺk. Alebo máme záhradku s jednou stranou dlhou 10m a druhou 20m. Plocha záhradky je 200m². Až teraz dostalo násobenie svoj význam. Takisto je to aj so skalárnym súčinom.

Vysvetlenie na príklade

Napadlo nám, že možno sa ti to naše vysvetlenie stále zdá abstraktným, niečím neuchopiteľným. A tak ti skúsime vysvetliť skalárny súčin ešte raz, na jednom z jeho použití. Na množstve vykonanej práce. Prácu o veľkosti jedného J (Joul) vykonáme vtedy, keď ťaháme nejakú vec po dráhe jeden meter silou jeden N (Newton).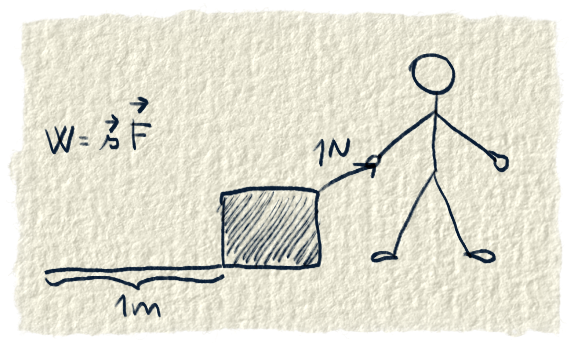

Hovoria ti niečo Železné vráta? Je to roklina, ktorú vyhĺbil Dunaj v Karpatoch medzi Srbskom a Rumunskom. Rieka je tu veľmi úzka a hlboká. Veľké bralá nie sú len okolo rieky, ale sú aj pod hladinou. Vytvárajú silné protiprúdy. Tak silné, že lode idúce po prúde Dunaja nemohli kedysi tadiaľ prejsť. Musel ich ťahať vlak.

Aby bolo možné túto nebezpečnú trať dobre navrhnúť, museli vtedajší inžinieri určite rátať tak, aby vlak musel vykonať čo najmenej práce. Teda museli vedieť vypočítať prácu.

Loď išla rovno, v smere rieky, ale vlak ju neťahal úplne rovno. Išiel vedľa nej a tak ju ťahal trochu šikmo. Z tohto môžeme usúdiť, že dráha aj sila sú vektory. Obe majú veľkosť a smer.

Prácu, ktorú vlak vykoná, keď ťahá loď vypočítame ako sila krát dráha. Pretože každý jeden meter dráhy musel vlak ťahať loď danou silou. Teda každý jeden meter musíme pripočítať veľkosť sily.

No sila nás nebude zaujímať celá. Pretože ona nie celá pôsobí v smere tej dráhy. Časť z nej pôsobí aj do boku a vôbec nepomáha ísť lodi dopredu.

Skutočnú prácu vykoná iba časť sily, ktorá ide tým istým smerom ako loď. Každý jeden meter teda nepripočítavame celú silu, ale iba tú časť, ktorá loď naozaj ťahá dopredu.

Užitočnú časť sily dostaneme pomocou goniometrie.

Nepripadá ti to ako skalárny súčin? Pretože je to on. Tu sme počítali spoločný účinok dráhy a sily. Teda ako veľmi tieto dva vektory spolu pôsobia.

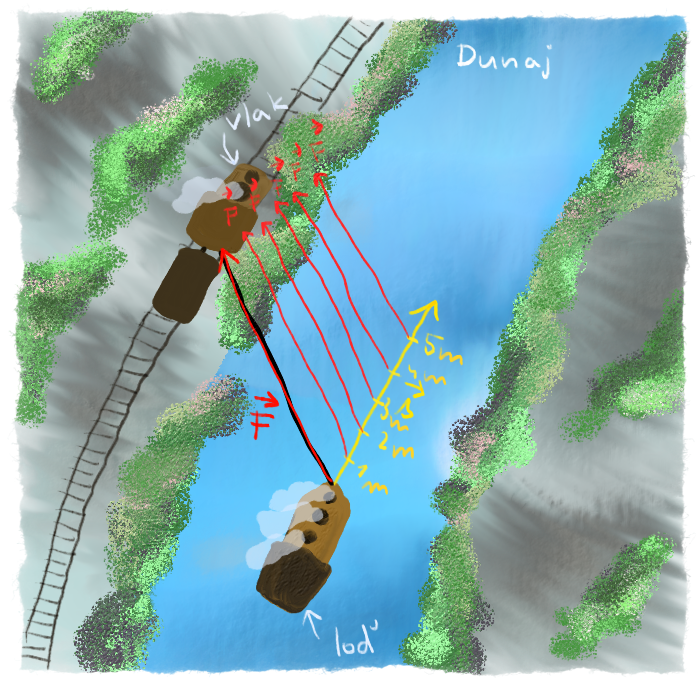
Použitie skalárneho súčinu

Už určite vieš, že sa ním počíta práca. Okrem nej sa vo fyzike dá skalárnym súčinom vyrátať napríklad aj výkon. V počítačoch sa používa pri spracovaní obrázkov, zvuku alebo v neurónových sieťach. Počítajú s ním aj ľudia, ktorí robia počítačové hry. Ďalšie aplikácie sú v matematike samotnej. Napríklad vyrátanie uhla medzi vektormi, projekcia jedného vektora na druhý alebo zistenie rovnobežnosti/kolmosti dvoch vektorov.

Zdroje