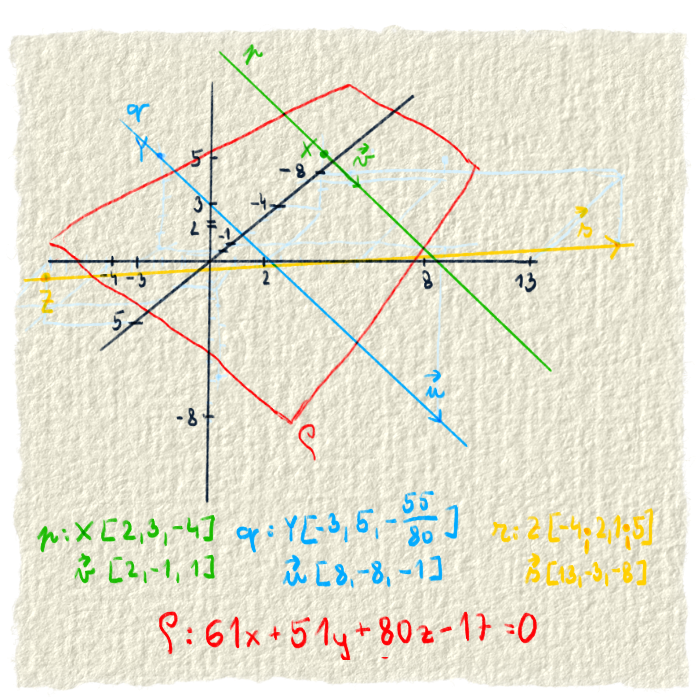
Vzájomná poloha priamky a roviny

Rovina a priamka majú voči sebe tri druhy polôh. Priamka patrí rovine, priamka je rovnobežná s rovinou a priamka je rôznobežná s rovinou.

V prípade, že priamka leží na rovine, je možné, že ťa zvedie povedať, že priamka je totožná s rovinou. Na toto si daj pozor, je to zle. Všetky body priamky síce môžeš nájsť na rovine, ale nie všetky body roviny sú na priamke. Priamka a rovina nie sú rovnaké a slovo totožné znamená, že rovnaké sú.

Pozri sa na obrázok č. 1 a skús porozmýšľať, podľa čoho by sme mohli rozlíšiť vzájomné polohy priamky a roviny. Ak už máš rozmyslené, môžeš čítať ďalej. Možno si tipoval, že je to počet spoločných bodov a myslel si si správne.

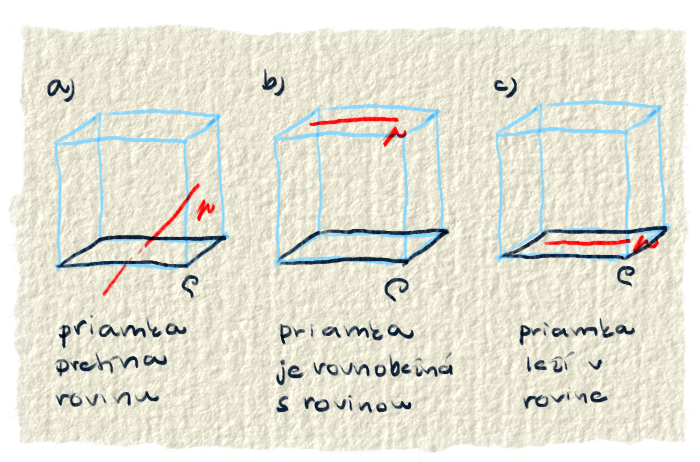
Ak je priamka rovnobežná s rovinou, nemajú ani jeden bod spoločný. Ak je priamka rôznobežná s rovinou, tak niekde priamka rovinu pretína a teda majú iba jeden bod spoločný. V prípade, že priamka patrí rovine, tak majú spoločných nekonečne veľa bodov (každý bod, ktorý je na priamke, patrí aj rovine).

Chceme teda zistiť, koľko bodov majú priamka a rovina spoločných. Pohybujeme sa v priestore, takže všetky body na priamke dostaneme pomocou jej parametrickej rovnice. Všetky body na rovine vieme dostať viacerými rovnicami, ale vyberieme si všeobecnú rovnicu roviny. Bude sa nám ľahšie počítať.

Ešte treba zistiť, či majú nejaké body rovnaké. Otázku trochu preformulujeme a spýtame sa, či niektoré body priamky patria aj rovine. Využijeme všeobecnú rovnicu roviny. Tá hovorí o tom, či nejaký bod patrí alebo nepatrí rovine. Ak rovine patrí, obe strany všeobecnej rovnice roviny budú rovné nule a bod do roviny patrí. Ak budú strany rozdielne, bod do roviny nepatrí.

Už máme nástroj, ktorým zistíme, či nejaký bod do roviny patrí alebo nie. Chceli sme vedieť, či majú priamka a rovina nejaké body spoločné, teda či nejaké body priamky patria rovine. Body na priamke máme vyjadrené parametrickou rovnicou priamky. Dosadíme ich do všeobecnej rovnice priamky, vypočítame a tešíme sa z výsledku.

Po dosadení rovnice priamky do rovnice roviny, budeme mať jednu neznámu - parameter t. Ak ho vypočítame a dosadíme do rovnice priamky, dostaneme bod, v ktorom sa priamka a rovina pretínajú. Vtedy hovoríme, že priamka a rovina sú rôznobežné. Parameter však môže aj vypadnúť a rovnica môže byť na oboch stranách nula. To znamená, že za t môžeme dosadiť hocijaké číslo a bod bude stále patriť priamke. Každý bod priamky teda patrí aj rovine a môžeme povedať, že priamka patrí rovine. Pri poslednom type výsledku parameter znovu vypadne, ale na každej strane rovnice bude iné číslo. To znamená, že za t nedokážeme dosadiť nič. Parameter nemáme a tak nevieme dostať ani jeden bod na priamke. Znamená to, že priamka a rovina nemajú nič spoločné a teda sú rovnobežné.

Vyskúšame si to na príklade: