Vektory

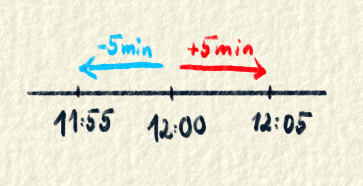
Vetu: "Prídem o päť minút." ti už niekto povedal aspoň stokrát. Keď to počuješ, pozrieš na hodinky s cieľom zistiť, kedy kamarát príde. Ak máš na hodinkách 12:00 vieš, že kamarát príde 12:05. Ak ukazujú 8:53, kamarát bude u teba 8:58.

Tých 5 minút je z matematického hľadiska vektor, pretože predstavuje zmenu. Čas 12:00 je bod, kde sa vektor aplikuje. Keď teda aplikujeme vektor 5 minút na čas 12:00, zmení sa nám tento čas na 12:05. Keď ten istý vektor aplikujeme na čas 8:53, tak budeme mať 8:58. Keď vektor 15 minút aplikujeme na čas 12:00, budeme mať čas 12:15. Môžeme mať aj záporný vektor, napríklad -5 minút. Keď aplikujeme ten na čas 12:00, dostaneme 11:55. Vektor môže mať teda veľkosť aj smer. Veľkosť je počet minút (napr. 5 min) a smer je + alebo -.

Príklad s časom bol vektor v jednorozmernom priestore (iba na osi x). Vektory samozrejme existujú aj v 2D a 3D.

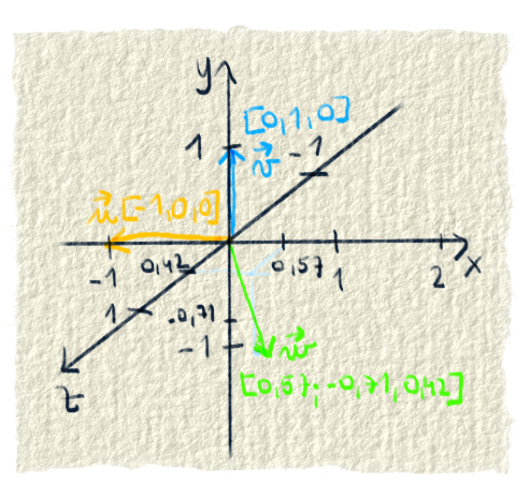
Ako sme si už povedali, vektor je zmena polohy bodu. Pre viacrozmerný priestor je to zmena po každej osi. Zapisujeme ju do hranatých zátvoriek, podobne ako bod. V 3D priestore by vektor mohol byť takýto: [3,8,-1]. Znamená to, že bod sa zo svojho miesta pohne o 3 kroky na osi x, o 8 krokov na osi y a o -1 krok na osi z.

Vektory sa zvyčajne označujú malými písmenami u,v,w, nad ktorými sa píše šípočka: $\vec{u}$, $\vec{v}$, $\vec{w}$. Niekde ich označujú tučným písmom: u,v,w. Veľkosť vektora sa označuje rovnými zátvorkami $|\vec{v}|$.

Vektor má veľkosť a smer. Veľkosť vektora znamená, že ako veľa pohnem bod. Smer vektora je smer, ktorým sa bod pohne. Na papier sa kreslí vektor ako šípka. Veľkosť šípky je veľkosť vektora a smer šípky je smer vektora.

Vektor sa kreslí medzi dvomi bodmi. Bod na začiatku vektora je ten, z ktorého vychádzame a bod na konci vektora je ten, do ktorého prídeme. Tieto dva body však nie sú samotný vektor. Vektor je tá šípka/cesta/zmena medzi nimi. Vychádzať môžeme z hocijakého bodu a prísť tiež do hocijakého bodu. Ak sa však pohneme o rovnaký úsek, rovnakým smerom, je to stále ten istý vektor, nech sa pohneme skadiaľkoľvek. Vektor je teda daný veľkosťou a smerom, nie pozíciou.

Posunutie vektora na začiatok sústavy

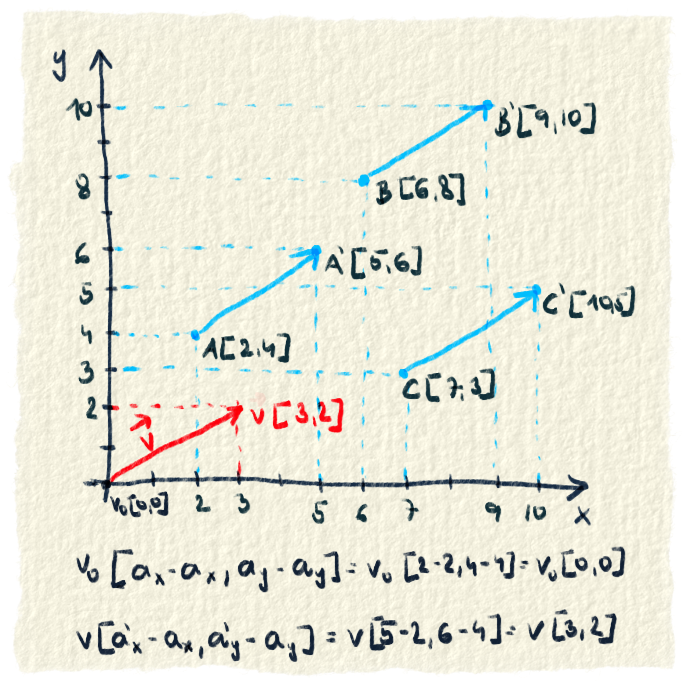
Kúsok ďalej budeme počítať veľkosť vektora, sčítavať vektory a robiť s nimi rôzne operácie. Na to potrebujeme vedieť, ako je vektor dlhý po všetkých osiach. Teda koľko dielikov zaberá na osi x, koľko na y a koľko na osi z.

Počet dielikov zistíme tak, že od koncového bodu vektora odpočítame začiatočný bod. Tým ho vlastne posunieme do bodu 0,0. Súradnice koncového bodu vektora nám povedia, koľko dielikov je vektor dlhý. Pri posúvaní vektora musíme samozrejme odpočítať aj začiatočný bod od seba samého, aby vektor začínal v bode [0,0].

Na obrázku môžeš vidieť vektor na troch rôznych miestach, ktorý sme posunuli do bodu [0,0]. Výpočet je spravený pre začiatočný bod A a koncový bod A’.

Takže vždy, keď budeme robiť nejaké operácie s vektormi, posunieme si ich tak, aby začínali v bode [0,0]. Vďaka tomu sa môžeme spoľahnúť na to, že súradnice vektora nám hovoria o počte dielikov na jednotlivých osiach.

Veľkosť a smer vektora

Zatiaľ sme hovorili iba to, že vektor udáva nejaký smer a veľkosť ako sa treba pohnúť. Nevieme nič presné, ani presne o koľko a ani presne kam. Vieme to vypočítať zo súradníc jeho koncového bodu, keď začína v bode [0,0]. Posunúť vektor na začiatok sústavy už vieš, tak môžeme ísť smelo počítať veľkosť a smer vektora.

Smer je jednoduchý. Sú to súradnice jeho koncového bodu. Veľkosť vektora je vzdialenosť medzi jeho začiatočným a koncovým bodom. Vieme ju vypočítať pomocou Pytagorovej vety, lebo poznáme vzdialenosť medzi týmito bodmi aj na osi x aj na osi y.

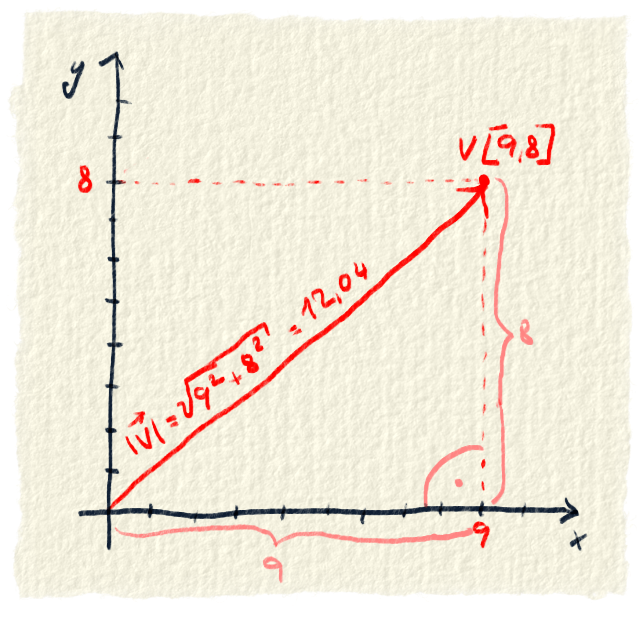
Umiestnenie vektora

Pri vektoroch sa môžeš stretnúť so slovami kolineárny a komplanárny. Na prvé počutie to znie dosť zložito, ale tieto dve slová iba pomenúvajú umiestenie vektorov. Keď hovoríme, že vektory sú kolineárne, myslíme tým, že vektory sú rovnobežné.

Kolineárne vektory môžeme ešte rozdeliť na súhlasné a nesúhlasné. Súhlasné vektory idú rovnobežne, rovnakým smerom. Nesúhlasné vektory sú tiež rovnobežné, ale idú opačným smerom.

Komplanárne vektory sú také, ktoré ležia v rovnobežných rovinách.

Násobenie vektora číslom

Vektor môžeme vynásobiť hocijakým číslom. Po násobení sa zmení veľkosť vektora. Vektor najprv posunieme na začiatok súradnicovej sústavy a potom jeho koncové súradnice vynásobíme nejakým číslom. Dostaneme nové súradnice, ktoré budú určovať vynásobený vektor.

Keď násobíme vektor kladným číslom väčším ako 1, bude dlhší. Keď je to kladné číslo medzi 0 a 1, vektor sa skráti. Keď sa násobí záporným číslom, vektor bude mať opačný smer.

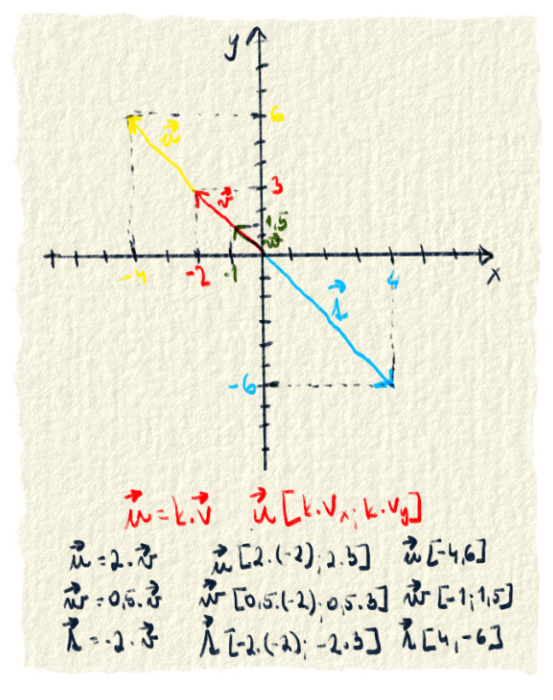
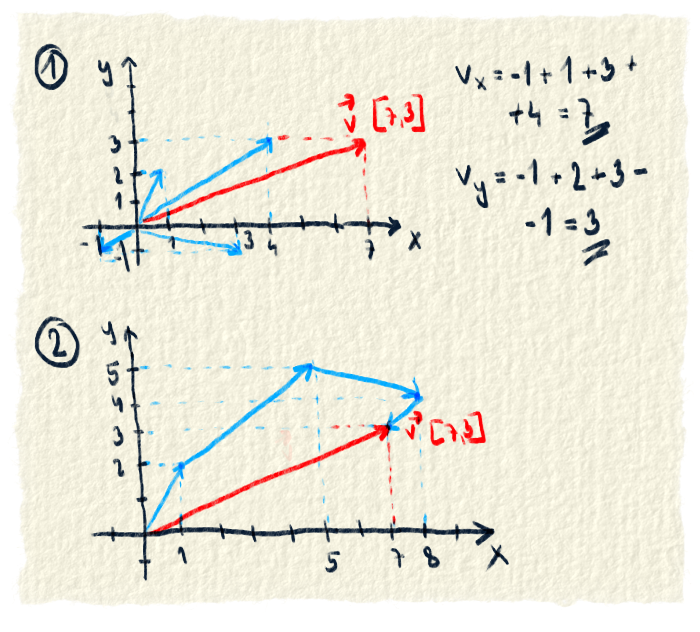
Sčítavanie vektorov

Vektory, ktoré ideme sčítavať, najprv presunieme na začiatok sústavy. Potom sčítame ich koncové súradnice na jednotlivých osiach. Teda sčítame súradnice vektorov na osi x, na osi y a ak treba, aj na osi z. Vznikne nám jeden nový vektor. Keď nejaký bod posunieme o tento nový vektor, dostaneme ho na to isté miesto, ako keby sme ho posunuli o každý starý vektor.

Na obrázku sú štyri modré vektory, ktoré chceme sčítať. Po ich zrátaní vznikne výsledný vektor, ktorý je nakreslený červenou. V prvej časti výsledný vektor dostaneme tak, že sčítame x a y súradnice modrých vektorov. Je jedno, s ktorým vektorom začneme a ktorými pokračujeme, výsledok je vždy rovnaký. V druhej časti je ukázané sčítavanie vektorov tak, že bod sa posunie najprv o prvý vektor, potom o druhý, o tretí, o štvrtý. Tu je tiež jedno, ktorým vektorom začneme.

Skalárny súčin

V polovici 19. storočia sa ujo Hamilton zaoberal niečím, čo sa nazýva "quaternion". Pri skúmaní quaternion-ov objavil vec, ktorú dnes voláme skalárny súčin. Táto vec sa neskôr adaptovala do vektorov.

Skalárny súčin je jeden zo spôsobov ako spolu vynásobiť dva vektory. Výsledok skalárneho súčinu je číslo a hovorí o tom, ako veľmi sú vektory rovnobežné. Teda ako veľmi pôsobí jeden vektor v smere druhého. Keď chceme povedať, že dva vektory sa násobia skalárnym súčinom, znamienko súčinu je bodka. Skalárny súčin môžeme vyjadriť dvomi rôznymi spôsobmi. Algebraickým a geometrickým.

Geometrický: vyjadríme ho pomocou uhla medzi vektormi $$ \vec{u} \cdot \vec{v} = |\vec{u}| |\vec{v}| cos \alpha $$ Algebraický: vyjadrí sa pomocou súradníc $$ \vec{u} \cdot \vec{v} = u_{x} v_{x} + u_{y} v_{y}$$

V praxi je niekedy treba zistiť uhol medzi dvomi vektormi. Tu prichádza na scénu skalárny súčin, pretože vďaka nemu vieme uhol vypočítať. Geometrickú a algebraickú podobu skalárneho súčinu vieme dať do rovnosti. Následne si z toho odvodíme kosínus uhla medzi vektormi. (Pozor, výsledok je kosínus uhla a nie samotný uhol. Keď treba vypočítať uhol, tak výsledok ešte musí ísť do funkcie arkuskosínus (arccos)) $$ \begin{equation} \displaylines{ u_{x} v_{x} + u_{y} v_{y} = |\vec{u}| |\vec{v}| cos \alpha \\ \frac{u_{x} v_{x} + u_{y} v_{y}}{|\vec{u}| |\vec{v}| } = cos \alpha } \end{equation} $$ Keď sú dva vektory rovnobežné, uhol medzi nimi je 0°. Výsledkom cos0° je 1. Keď sú vektory na seba kolmé, uhol medzi nimi je 90°. Výsledok cos90° je 0. Ak by si náhodou potreboval vyhľadať skalárny súčin na nete aj v angličtine, tak po anglicky sa to povie dot product.

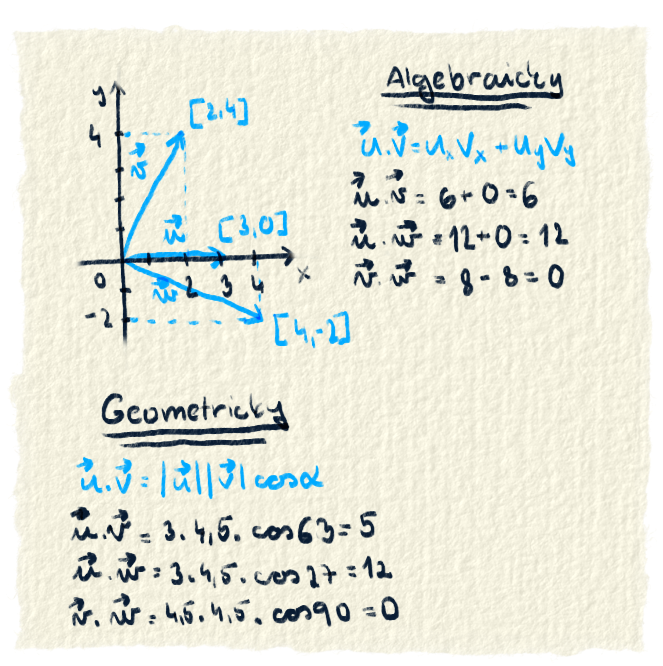
Vektorový súčin

Vektorový súčin vznikol rovnako ako skalárny. To isté storočie, ten istý ujo, ten istý problém. Prvé najslávnejšie použitie vektorového súčinu bolo v rovniciach uja Maxwella, ktoré hovoria dačo o elektromagnetizme.

Z vektorového súčinu sa tiež dozvieme niečo o tom, ako veľmi sú vektory na seba kolmé. Ako bonus získame vektor kolmý na tieto dva vektory, pretože výsledkom vektorového súčinu je vektor. Vektorový súčin sa robí v 3D priestore (v 2D nedáš dva vektory a ešte aj tretí kolmý na ne). Znamienko súčinu je $\times$, lebo ho treba odlíšiť od skalárneho súčinu.

Rovnako ako skalárny súčin má algebraickú a aj geometrickú formu.

Algebraický tvar: vyjadrí sa pomocou súradníc Geometrický tvar: vyjadrí sa pomocou uhla medzi vektormi $$ \vec{v} \times \vec{u} = |\vec{v}| \cdot |\vec{u}| \cdot sin \alpha \cdot \vec{n} $$ Tu sa možno zarazíš nad dvomi vecami. Vec prvá, že ako sa dá vypočítať veľkosť vektora v 3D. Dá sa to rovnako ako v 2D, lebo Pytagorova veta funguje skrz všetky priestory (aj tie viac rozmerné ;) ). Veľkosť vektora v 3D sa vypočíta takto: $$ |\vec{v}| = \sqrt{v_{x}^2 + v_{y}^2 + v_{z}^2} $$ Vec druhá je ten vektor $\vec{n}$ na konci vzorca. To je jednotkový vektor kolmý na naše dva vektory. O jednotkovom vektore sa pobavíme neskôr.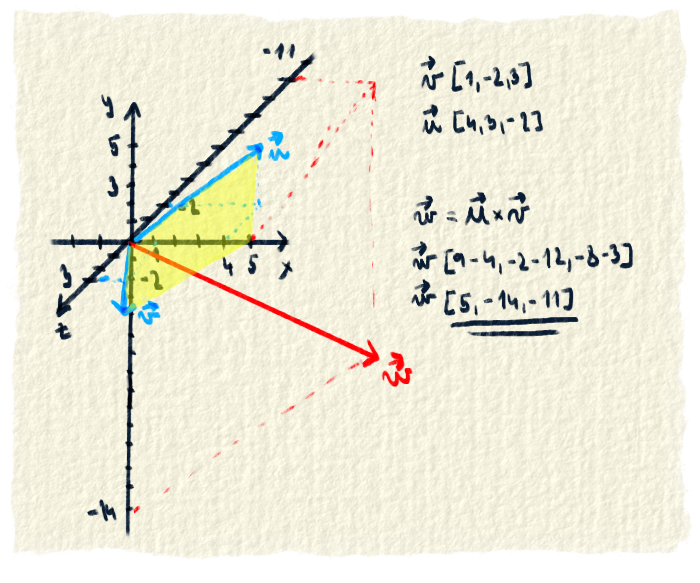

Čím viac sú násobené vektory na seba kolmé, tým väčší bude výsledný vektor. Keď sú násobené vektory rovnobežné, výsledný vektor je nulový (má súradnice [0,0,0]). Vektorový súčin nájdeš v angličtine ako cross product.

Jednotkový a normálový vektor

Sú to vektory, ktoré dostali mená, lebo sa často používajú.

Normálový vektor je taký vektor, ktorý je na niečo kolmý. Je jedno, či na iný vektor/y, priamku, plochu. Skratka slovami normálový vektor sa označuje vektor, ktorý je na niečo kolmý.

Jednotkový vektor je vektor, ktorý má dĺžku 1.

Zhrnutie

Vektor je niečo, čo ukazuje smer, ktorým sa má bod pohnúť a aj ako veľmi sa má pohnúť. Aby sa s vektormi ľahšie počítalo, treba ich presunúť do začiatku súradnicovej sústavy. Vektory vieme sčítať a vieme ich aj násobiť. Vektor môžeme násobiť jedným číslom a to tak, že tým číslom vynásobíme každú súradnicu. Týmto meníme veľkosť vektora, vieme ho skrátiť alebo natiahnuť. Vektory sa dajú násobiť aj medzi sebou a to dvomi spôsobmi. Skalárnym alebo vektorovým súčinom. Z oboch súčinov vieme zistiť to, ako veľmi sú vektory rovnobežné (resp. kolmé). Výsledkom skalárneho súčinu je číslo a výsledok vektorového súčinu je vektor.